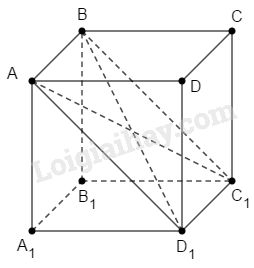
a) Ta có \(AB // CD\) và \(AB = CD\) (vì \(ABCD\) là hình chữ nhật).
\(CD // C_1D_1\) và \(CD = C_1D_1\).
Suy ra: \(AB // C_1D_1\) và \(AB = C_1D_1\).
Do đó tứ giác \(ABC_1D_1\) là hình bình hành nên \(AC_1\) và \(BD_1\) cắt nhau (hai đường chéo hình bình hành cắt nhau tại trung điểm mỗi đường).
b) Vì các điểm \(A, C, C_1\) và \(A_1\) cùng thuộc \(mp(ACC_1A_1)\) mà \(ACC_1A_1\) là một hình chữ nhật nên \(AC_1\) cắt \(A_1C.\)
c) Vì \(BD_1\) không thuộc \(mp(ADD_1A_1)\), không thuộc \(mp(ABB_1A_1)\) và cũng không thuộc \(mp(ACC_1A_1)\) nên \(BD_1\) và \(AA_1\) không cắt nhau.