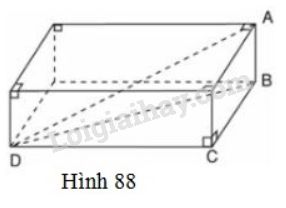
Bài 12 trang 104 SGK Toán 8 tập 2
Lời giải
Bài Tập và lời giải
A. Hoạt động cơ bản - Bài 19C: Cách nối các vế câu ghép - Kết bài trong bài văn miêu tả người
Giải bài 19C: Cách nối các vế câu ghép - Kết bài trong bài văn miêu tả người phần hoạt động cơ bản trang 14 sách VNEN Tiếng Việt 5 với lời giải dễ hiểu
B. Hoạt động thực hành - Bài 19C: Cách nối các vế câu ghép - Kết bài trong bài văn tả người
Giải bài 19C: Cách nối các vế câu ghép - Kết bài trong bài văn tả người phần hoạt động thực hành trang 14, 15 sách VNEN Tiếng Việt 5 với lời giải dễ hiểu
C. Hoạt động ứng dụng - Bài 19C: Cách nối các vế câu ghép - Kết bài trong bài văn tả người
Giải bài 19C: Cách nối các vế câu ghép - Kết bài trong bài văn tả người phần hoạt động ứng dụng trang 16 sách VNEN Tiếng Việt 5 với lời giải dễ hiểu