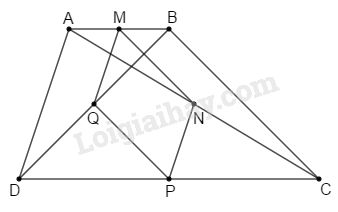
a) \(M, N, P, Q\) theo thứ tự là trung điểm của \(AB, AC, CD, BD\) nên \(MN\) là đường trung bình của \(\Delta ABC\); \(QP\) là đường trung bình của \(\Delta BCD\).
Suy ra:
\(\begin{array}{l}MN//BC;MN = \dfrac{1}{2}BC\\QP//BC;QP = \dfrac{1}{2}BC\end{array}\)
Xét tứ giác \(MNPQ\) có \(MN // QP\) (cùng song song với \(BC\)); \(MN = QP = \dfrac{1}{2}BC\)
\(⇒ MNPQ\) là hình bình hành (theo dấu hiệu nhận biết hình bình hành).
b) \(M;Q\) lần lượt là trung điểm của \(AB;BD\) nên \(MQ\) là đường trung bình \(\Delta ABD\).
\(\Rightarrow MQ//AD;MQ = \dfrac{1}{2}AD\).
\(ABCD\) là hình thang cân thì \(AD=BC\) do đó \(MN = MQ = \dfrac{1}{2}BC = \dfrac{1}{2}AD\).
Do đó hình bình hành \(MNPQ\) có hai cạnh kề bằng nhau nên là hình thoi.
c) \(MNPQ\) là hình vuông thì \(MQ\bot MN\) hay \(BC\bot AD\).
Gọi \(E\) là giao điểm của \(AD\) và \(BC\).
Khi \(MNPQ\) là hình vuông thì \(\Delta ECD\) là tam giác vuông tại \(E\).
Lại có \(MNPQ\) là hình vuông thì \(MQ=MN\) thì \(ABCD\) là hình thang cân nên \(\widehat D = \widehat C\) do đó \(\Delta ECD\) là tam giác vuông cân tại \(E\).
Vậy hình thang \(ABCD\) là hình thang cân có \(\widehat D = \widehat C = {45^o}\) thì \(MNPQ\) là hình vuông.