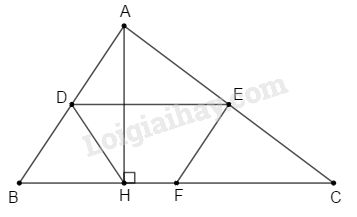
a) \(DE\) là đường trung bình của \(\Delta ABC\) nên \(DE//BC;DE = \dfrac{1}{2}BC\).
Tứ giác \(DECH\) có \(DE//HC\) nên là hình thang.
Tứ giác \(BDEF\) có \(DE//BF; DE=BF= \dfrac{1}{2}BC\) nên là hình bình hành.
Xét tam giác \(AHC\) vuông tại \(H\), đường trung tuyến ứng \(HE\) ứng với cạnh huyện \(AC\) nên \(HE = \dfrac{1}{2}AC\).
\(DF\) là đường trung bình của \(\Delta ABC\) nên \(DF//AC;DF = \dfrac{1}{2}AC\).
Tứ giác \(DEFH\) có \(DE//HF\) và \(DF = HE = \dfrac{1}{2}AC\) nên là hình thang cân.
b) \(BC=HB+HC=4+6=10 \;(cm)\).
\(BF=FC=DE=BC:2=10:2\)\(\,=5\;(cm)\).
\(HF=BF-BH=5-4=1\;(cm)\).
Hình thang \(DEFH\), hình thang \(DECH\) và hình bình hành \(BDEF\) có cùng chiều cao bằng \(\dfrac{1}{2}AH = \dfrac{1}{2}.8 = 4\,cm\).
Diện tích của hình thang \(DEFH\) là:
\({S_{DEFH}} = \dfrac{1}{2}.\left( {1 + 5} \right).4 = 12\,\left( {c{m^2}} \right)\)
Diện tích hình thang \(DECH\) là:
\({S_{DECH}} = \dfrac{1}{2}.\left( {5 + 6} \right).4 = 22\,\left( {c{m^2}} \right)\)
Diện tích hình bình hành \(BDEF\) là:
\({S_{BDEF}} = 4.5 = 20\,\left( {c{m^2}} \right)\)
c) Áp dụng định lí Pytago vào tam giác vuông \(AHC\), ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} = {8^2} + {6^2} = 100\\ \Rightarrow AC = \sqrt {100} = 10\end{array}\)
\(HE = \dfrac{1}{2}AC = \dfrac{1}{2}.10 = 5\,\left( {cm} \right)\).