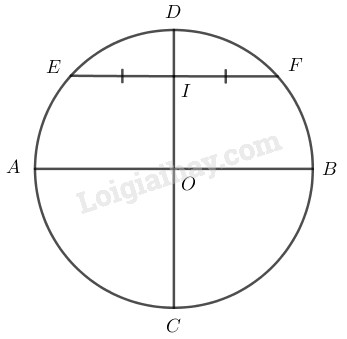
Giả sử trên hình thực ta có đường tròn tâm \(O\) cùng với hai đường kính vuông góc của đường tròn đó là \(AB\) và \(CD\).
Ta vẽ thêm một dây cung \(EF\) song song với \(AB\).
Khi đó đường kính \(CD\) sẽ đi qua trung điểm \(I\) của đoạn \(EF\).
Từ đó ta suy ra cách vẽ sau đây:
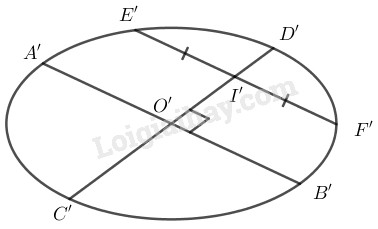
- Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính \(A’B’\) của hình elip đó. Đường kính này đi qua tâm \(O’\) của elip.
- Vẽ một dây cung \(E’F’\) song song với đường kính \(A’B’\).
- Gọi \(I’\) là trung điểm của \(E’F’\). Đường thẳng \(O’I’\) cắt elip tại hai điểm \(C’\) và \(D’\). Ta có \(A’B’\) và \(C’D’\) là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
Nhận xét. Hình bình hành \(A’C’B’D’\) là hình biểu diễn của hình vuông \(ACBD\) nội tiếp trong một đường tròn.