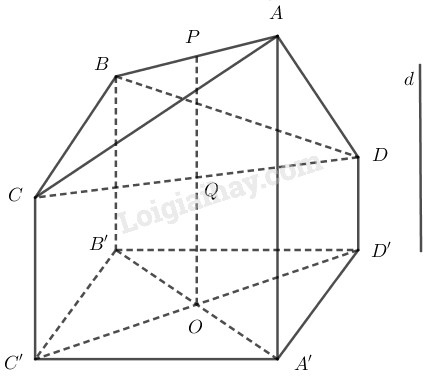
Cho tứ diện \(ABCD\). Gọi \(d\) là một đường thẳng không song song với với các cạnh của tứ diện và \(\left( \alpha \right)\) là một mặt phẳng cắt \(d\). Gọi \(A’\), \(B’\), \(C’\), \(D’\) lần lượt là hình chiếu của \(A\), \(B\), \(C\), \(D\) trên mặt phẳng \(\left( \alpha \right)\). Gọi \(P\) và \(Q\) lần lượt là trung điểm của hai cạnh đối diện \(AB\) và \(CD\). Khi đó hình chiếu của \(P’\) và \(Q’\) của \(P\) và \(Q\) sẽ lần lượt là trung điểm của \(A’B’\) và \(C’D’\).
Muốn cho \(A’\), \(B’\), \(C’\), \(D’\) là các đỉnh của một hình bình hành ta chỉ cần chọn phương chiếu d sao cho \(d\) song song với đường thẳng \(PQ\).
Vậy để hình chiếu song song của một tứ diện là một hình bình hành ta có thể chọn :
- Phương chiếu d là phương của một trong ba đường thẳng đi qua trung điểm của hai cạnh đối diện của tứ diện cho trước.
- Mặt phẳng chiếu \(\left( \alpha \right)\) là mặt phẳng tùy ý, nhưng phải cắt đường thẳng \(d\).