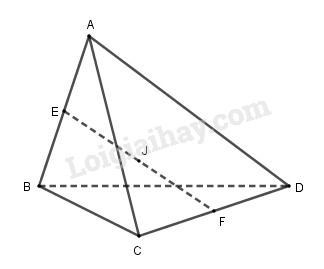
Gọi \(\displaystyle E, F\) lần lượt là trung điểm của \(\displaystyle AB\) và \(\displaystyle CD\). Ta có:
\(\displaystyle M{A^2} + M{B^2} = 2M{E^2} + {1 \over 2}A{B^2}\,\,\,\,\,\left( 1 \right)\)
\(\displaystyle M{C^2} + M{D^2} = 2M{F^2} + {1 \over 2}C{{\rm{D}}^2}\,\,\,\,\,\left( 2 \right)\)
Cộng (1) và (2) ta có:
\(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\)
\(\displaystyle = 2\left( {M{E^2} + M{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}\,\,} \right)\,\,\)
Gọi \(\displaystyle J\) là trung điểm của \(\displaystyle EF\), ta có:
\(\displaystyle \left( {M{E^2} + M{F^2}} \right) = 2M{J^2}\, + {1 \over 2}E{F^2}\)
Khi đó:
\(\displaystyle \eqalign{
& M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2} \cr
& = 2\left( {2M{J^2}\, + {1 \over 2}E{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr
& \ge E{F^2} + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr} \)
Vậy \(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị nhỏ nhất khi \(\displaystyle M \equiv J\).