Xét \(\Delta ABC\) và \(\Delta CDA\) có:
\(AC\) chung
\(AB=CD\) (gt)
\(BC=DA\) (gt)
\( \Rightarrow \Delta ABC = \Delta CDA\) (c.c.c)
Do đó:
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{C_2}}\\\widehat {{A_2}} = \widehat {{C_1}}\\\widehat B = \widehat D\end{array}\)
(các góc tương ứng).
Bài 3.2
a) Vẽ tam giác \(ABC\) có \(BC = 2cm, AB = AC = 3cm.\)
b) Gọi \(E\) là trung điểm của cạnh \(BC\) của tam giác \(ABC\) trong câu a). Chứng minh rằng \(AE\) là tia phân giác của \(BAC.\)
Phương pháp:
a) Dựng tam giác \(ABC\) biết \(AB=c;BC=a;AC=b\)
- Vẽ đoạn \(BC= a\)
- Trên cùng một nửa mặt phẳng bờ \(BC\) vẽ cung tròn tâm \(B\) bán kính \(c\) và cung tròn tâm \(C\) bán kính \(b\).
- Hai cung tròn cắt nhau tại \(A\).
- Vẽ các đoạn \(AB,AC\), ta được tam giác \(ABC\).
b) Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
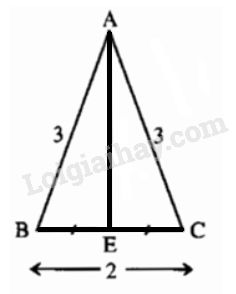
a)
- Vẽ đoạn \(BC= 2cm\)
- Trên cùng một nửa mặt phẳng bờ \(BC\) vẽ cung tròn tâm \(B\) bán kính \(3cm\) và cung tròn tâm \(C\) bán kính \(3cm\).
- Hai cung tròn cắt nhau tại \(A\).
- Vẽ các đoạn \(AB, AC\), ta được tam giác \(ABC\) cần dựng.
b) Xét \(ΔBAE\) và \(ΔCAE\) có:
\(AB = AC\) \((=3cm)\)
\(BE = EC\) (vì \(E\) là trung điểm của \(BC\))
\(AE\) chung
\(⇒ ΔBAE = ΔCAE\) (c.c.c)
\(⇒ \widehat {BAE} = \widehat {CAE}\) (hai góc tương ứng)
Vậy \(AE\) là phân giác của góc \(BAC.\)
Bài 3.3
Cho bốn điểm \(A, B, C, D\) thuộc đường tròn \((O)\) sao cho \(AB = CD.\) Chứng minh rằng \(\widehat {AOB} = \widehat {COD}\).
Phương pháp:
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
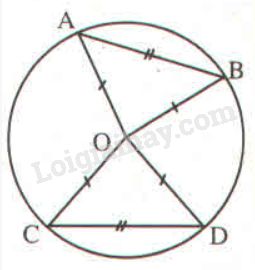
Xét \(ΔAOB\) và \(ΔCOD\) có:
\(OA = OC\) (cùng bằng bán kính đường tròn)
\(OB = OD\) (cùng bằng bán kính đường tròn)
\(AB = CD\) (gt)
\(⇒ ΔAOB = ΔCOD\) (c.c.c)
\(⇒\widehat {AOB} = \widehat {COD}\) (hai góc tương ứng).