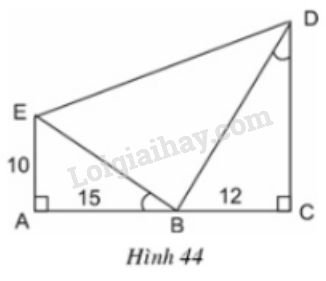
Bài 37 trang 79 SGK Toán 8 tập 2
Lời giải
Bài Tập và lời giải
A. Hoạt động thực hành - Bài 4C: Cảnh vật quanh em
Giải bài 4C: Cảnh vật quanh em phần hoạt động thực hành trang 46, 47 sách VNEN tiếng việt 5 với lời giải dễ hiểu
B. Hoạt động ứng dụng - Bài 4C: Cảnh vật quanh em
Giải bài 4C: Cảnh vật quanh em phần hoạt động ứng dụng trang 46 sách VNEN tiếng việt 5 với lời giải dễ hiểu