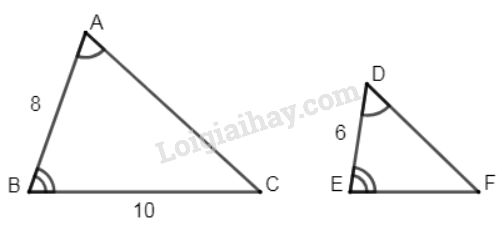
Bài 45 trang 80 SGK Toán 8 tập 2
Lời giải
Bài Tập và lời giải
A. Hoạt động cơ bản - Bài 7B: Âm thanh cuộc sống
Câu 1
Quan sát bức tranh về đập thuỷ điện Hoà Bình dưới đây:

B. Hoạt động thực hành - Bài 7B: Âm thanh cuộc sống
Giải 7B: Âm thanh cuộc sống phần hoạt động thực hành trang 74, 75, 76, 77 sách VNEN tiếng việt 5 với lời giải dễ hiểu
C. Hoạt động ứng dụng - Bài 7B: Âm thanh cuộc sống
Giải bài 7B: Âm thanh cuộc sống phần hoạt động ứng dụng trang 77 sách VNEN tiếng việt 5 với lời giải dễ hiểu