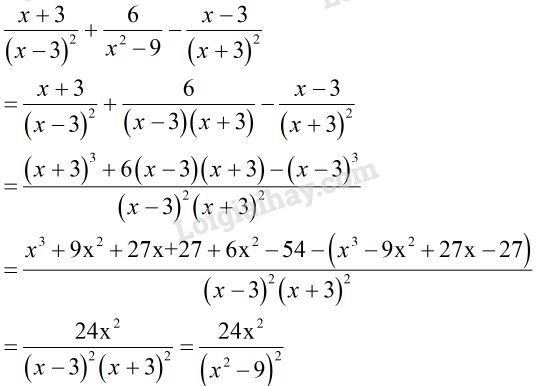Bài 4 trang 130 SGK Toán 8 tập 2
Lời giải
Bài Tập và lời giải
Em có dịp quan sát một buổi tập của lớp học võ buổi sáng ở công viên gần nhà. Hăy kể lại những gì em thấy ở buổi tập đó
Khu công viên rộng lớn. Cả khu vực như chìm trong giấc ngủ. Nhưng em đã lầm, vào đến bên trong, em mới thấy được sự hoạt động thầm lặng mà bền bỉ của mọi người.
Em đã có dịp theo bố đến tập thể dục buổi sáng tại một công viên. Em hãy kể lại những gì em nhìn thấy trong công viên buổi sáng đó
Đề bài: Em đã có dịp theo bố đến tập thể dục buổi sáng tại một công viên. Em hãy kể lại những gì em nhìn thấy trong công viên buổi sáng đó
Hãy tả cảnh một công viên mà em đã có dịp đến chơi
Đề bài: Hãy tả cảnh một công viên mà em đã có dịp đến chơi.Hướng dẫn: Các em có thể dựa theo dàn ý để viết thành bài miêu tả. Các em cũng có thể bổ sung thêm ý, thêm chi tiết cho bài viết được phong phú.
Lập dàn ý: Em hãy tả cảnh công vỉên mà em có dịp đến chơi
Tả bao quát: Công viên rộng lớn - hàng cây trong công viên - cây lá trong công viên - ghế đá trong công viên...
Em hãy tả cảnh một công viên mà em đã có lần đến thăm
Mãi đến tháng 6 năm 2004, em mới được đến thăm công viên Nguyễn Du ở trung tâm thành phố.