Khai triển hình trụ theo một đường sinh và trải phẳng ra, ta được một hình chữ nhật chiều rộng \(20cm\), chiều dài bằng chu vi đáy của cái lọ bằng \(10.3,14=31,4\; (cm).\)
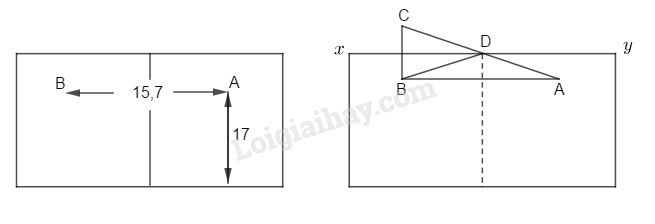
Ta cần chú ý đến vị trí con kiến và giọt mật. Ta cho con kiến ở điểm \(A\) cách đáy \(17cm\), thì giọt mật ở điểm \(B\) cũng cách đáy \(17cm\) và cách con kiến ở điểm \(A\) là nửa chu vi đáy của cái lọ bằng \(15,7 cm.\)
Dựng điểm \(C\) đối xứng với \(B\) qua đường \(xy\), nối \(AC\) cắt \(xy\) tại \(D\). Điểm \(D\) là điểm con kiến bò qua.
Vậy đoạn đường \(BDA\) là ngắn nhất.
Khi đó quãng đường con kiến cần đi là: \(BD+DA=2DA=AC\)
Tam giác \(ABC\) vuông tại \(B\), theo định lý Pi - ta - go ta có:
\(AC^2=AB^2+BC^2\) \(=15,7^2+6^2\) \( \Rightarrow AC = \sqrt {15,{7^2} + {6^2}} \approx 16,8\left( {cm} \right)\)