Bài 3. Hình cầu. Diện tích mặt cầu và thể tích hình cầu

Đề bài

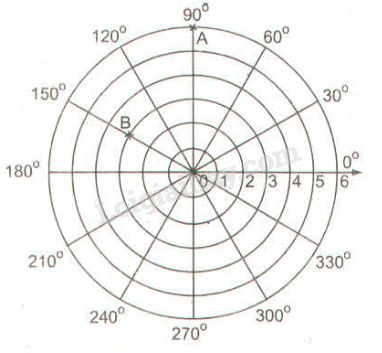
a) Trong hình \(102\), cho \(A\) là giao điểm của đường tròn \((0; 6)\) với tia \(90^o\) và kí hiệu là \(A(6; 90^o)\). Tương tự \(B\) là giao điểm của đường tròn \((0; 3)\) với tia \(150^o\) và kí hiệu là \(B(3; 150^o)\). Hãy đánh dấu các điểm \(C(6; 210^o), D(3; 30^o)\) và \(E(6; 330^o)\) trên hình \(102.\)

b) Nối \(AB, BC, AD, DE\) và \(BD\) em thấy hình gì?

Đề bài

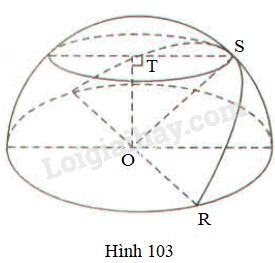
Trong nửa hình cầu có \(OR = x\; (cm),\) \(\widehat {TOS} = 45^o.\) Độ dài đoạn \(ST\) nhận giá trị nào trong các giá trị sau:

(A) \(x \;(cm);\)                 (B) \(\sqrt 2 x\; (cm)\)

(C) \(\displaystyle {x \over {\sqrt 2 }}\; (cm)\)             (D) \(2x \;(cm)\)

Đề bài

Trong các hình sau đây, hình nào có diện tích lớn nhất?

(A) Hình tròn có bán kính \(2cm\).

(B) Hình vuông có độ dài cạnh \(3,5cm\).

(C) Tam giác với độ dài các cạnh là \(3cm, 4cm, 5cm\).

(D) Nửa mặt cầu bán kính \(4cm\).

Hãy chọn kết quả đúng.

Đề bài

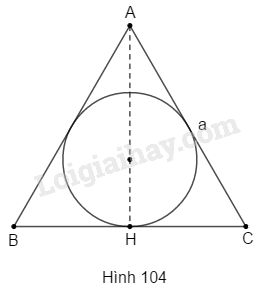
Cho hình quay một vòng xung quanh đường cao \(AH\) của tam giác đó, (xem hình 104), ta được một hình nón ngoại tiếp hình cầu. Tính thể tích phần hình nón bên ngoài hình cầu.

Đề bài

Hai hình cầu \(A\) và \(B\) có các bán kính tương ứng là \(x\) và \(2x\; (cm)\).

Tỉ số các thể tích của \(2\) hình cầu này là:

(A) \(1: 2\)            (B) \(1: 4\)         (C) \(1: 8\)

(D) Một kết quả khác.

Hãy chọn kết quả đúng.

Đề bài

Hình 105 minh họa: hình gồm một nửa hình cầu và một hình nón

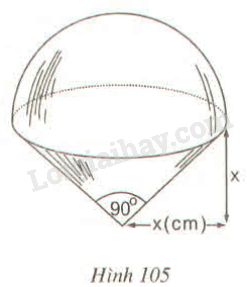
Thể tích của hình nhận giá trị nào trong các giá trị sau:

(A) \(\displaystyle {2 \over 3}\pi {x^3}(c{m^3})\)         (B) \(\displaystyle \pi {x^3}(c{m^3})\)

(C) \(\displaystyle {4 \over 3}\pi {x^3}(c{m^3})\)         (D) \(\displaystyle 2\pi {x^3}(c{m^3})\)

Đề bài

Một quả bóng hình cầu bên trong một hình lập phương như hình 106.

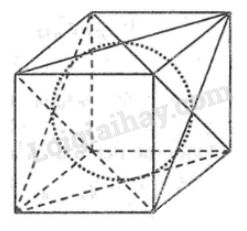
a) Tính tỉ số giữa diện tích toàn phần của hình lập phương với diện tích mặt cầu

b) Nếu diện tích mặt cầu là \(7\pi (c{m^2})\) thì diện tích toàn phần của hình lập phương là bao nhiêu?

c) Nếu bán kính hình cầu là \(4cm\) thì thể tích phần trống (trong hình hộp ngoài hình cầu) là bao nhiêu?

Đề bài

Sử dụng các thông tin và hình 107 để trả lời các câu hỏi sau:

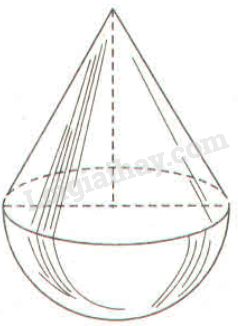
Mooth đồ chơi “lắc lư” của trẻ em gồm một hình nón gắn với nửa hình cầu (h.107) (chiều cao của hình nón bằng đường kính đường tròn đáy). Có hai loại đồ chơi: loại thứ nhất cao \(9cm\), loại thứ hai cao \(18cm\).

a) Tỉ số: \(\displaystyle{\text{thể tích đồ chơi loại thứ hai} \over \text{thể tích đồ chơi loại thứ nhất}}\)

(A) \(2\)                                   (C) \(8\)

(B) \(4\)                                   (D) \(16\)

Hãy chọn kết quả đúng.

b) Trong các số sau đây:

(A) \(2 (cm)\)                          (C) \(4 (cm)\)

(B) \( 3 (cm)\)                         (D) \(\displaystyle 4{1 \over 2}(cm)\)

Số nào là bán kính đường tròn đáy của đồ chơi loại thứ nhất?

c) Trong các số sau đây:

(A) \(30\pi \left( {c{m^3}} \right)\)           (B) \(36\pi \left( {c{m^3}} \right)\)

(C) \(72\pi \left( {c{m^3}} \right)\)           (D) \(610\left( {c{m^3}} \right)\)

Số nào là thể tích của loại đồ chơi thứ nhất?

Đề bài

Một hình cầu đặt vừa khít vào bên trong một hình tựa như hình 108 (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng \(\displaystyle {2 \over 3}\) thể tích hình trụ.

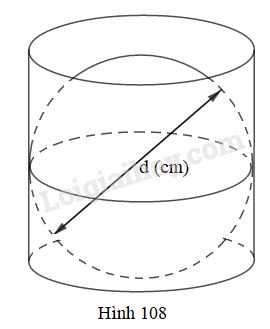
Nếu đường kính của hình cầu là \(d (cm)\) thì thể tích của hình trụ là:

(A) \(\displaystyle {1 \over 4}\pi {d^3}\left( {c{m^3}} \right)\)         (B) \(\displaystyle {1 \over 3}\pi {d^3}\left( {c{m^3}} \right)\)

(C) \(\displaystyle {2 \over 3}\pi {d^3}\left( {c{m^3}} \right)\)         (D) \(\displaystyle {3 \over 4}\pi {d^3}\left( {c{m^3}} \right)\)

Hãy chọn kết quả đúng.

Đề bài

Chọn dưa hấu.

Với hai quả dưa hấu (xem như là 2 hình cầu) một to và một nhỏ, tỉ số các đường kính của chúng là \(5: 4\), nhưng giá của quả to gấp rưỡi giá của quả nhỏ. Bạn chọn mua quả nào lợi hơn? (xem “chất lượng” của chúng là như nhau).

Đề bài

Đổ đầy nước vào một dụng cụ để đong có dạng hình nón, sau đó đổ hết lượng nước đó vào một hình trụ có bán kính đáy của hình nón và chiều cao bằng chiều cao của hình nón. Việc làm này lặp lại cho đến khi hình trụ đó đầy nước thì số lần múc đầy vào hình nón là:

(A) \(1\)                                  (C) \(3\)

(B) \(2\)                                  (D) \(4\)

Hãy chọn kết quả đúng.

Đề bài

Một khối gỗ dạng một hình trụ đứng, bán kính đường tròn đáy là \(r (cm)\), chiều cao \(2r (cm)\), người ta khoét rỗng hai nửa hình cầu như hình 109.

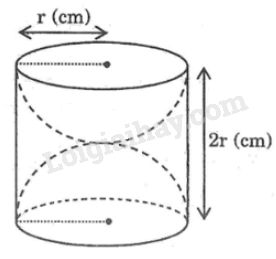
Như vậy diện tích toàn bộ của khối gỗ là:

(A) \(4\pi {r^2}\left( {c{m^2}} \right)\)        (B) \(6\pi {r^2}\left( {c{m^2}} \right)\)

(C) \(8\pi {r^2}\left( {c{m^2}} \right)\)        (D) \(10\pi {r^2}\left( {c{m^2}} \right)\)

Hãy chọn kết quả đúng.

Đề bài

Chiều cao của một hình trụ gấp ba lần bán kính đáy của nó.

Tỉ số của thể tích hình trụ này và thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ là:

(A) \(\displaystyle {4 \over 3}\)                                (C) \(\displaystyle {3 \over 1}\)

(B) \(\displaystyle {9 \over 4}\)                                (D) \(\displaystyle {4 \over 9}\)

Hãy chọn kết quả đúng.

Đề bài

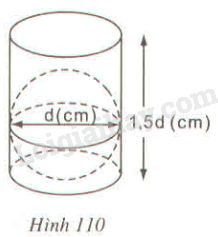
Một hình cầu đường kính \(d (cm) \) được đặt vào trong một hình trụ có chiều cao là \(1,5d (cm)\) như hình 110. Xét các phân số sau đây:

(A) \(\displaystyle{2 \over 3}\)                                (C) \(\displaystyle {2 \over 9}\)

(B) \(\displaystyle {4 \over 9}\)                                (D) \(\displaystyle {1 \over 3}\)

Đâu là tỉ số \(\displaystyle {{{V _\text{cầu}}} \over {{V _\text{trụ}}}}\)?