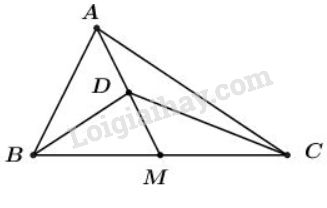
a) Vì \(M\) là trung điểm của \(BC\) nên:
Ta có:
\(\overrightarrow {DB} + \overrightarrow {DC} = 2\overrightarrow {DM} \)
Mặt khác, do \(D\) là trung điểm của đoạn \(AM\) nên \(\overrightarrow {DM} = - \overrightarrow {DA} \)
Khi đó: \(2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 2\overrightarrow {DA} + 2\overrightarrow {DM} \)\(= 2\left( {\overrightarrow {DA} + \overrightarrow {DM} } \right) = \overrightarrow 0 \)
b) Ta có:
\(\eqalign{
& 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \cr
& \Leftrightarrow 2\left( {\overrightarrow {OA} - \overrightarrow {OD} } \right) + \left( {\overrightarrow {OB} - \overrightarrow {OD} } \right) \cr&+ \left( {\overrightarrow {OC} - \overrightarrow {OD} } \right) = \overrightarrow 0 \cr
& \Leftrightarrow 2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \cr} \) (Đúng theo câu a)
Vậy: \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \), với \(O\) là điểm tùy ý