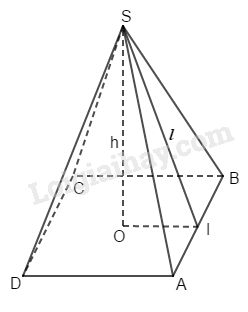
Áp dụng định lí Pytago vào tam giác vuông \(SOI\), ta có:
\(\begin{array}{l}S{I^2} = S{O^2} + O{I^2}\\ \Rightarrow OI = \sqrt {S{I^2} - S{O^2}} \\ \Rightarrow SO = \sqrt {S{I^2} - O{I^2}} \end{array}\)
Diện tích xung quanh hình chóp đều là:
\({S_{xq}} = 2.a.l\)
+) Nếu \(h=8;\;l=10\) thì ta có:
\(OI = \sqrt {{{10}^2} - {8^2}} = 6\) do đó \(a = 2OI = 2.6 = 12\)
\({S_{xq}} = 2.10.12 = 240\)
+) Nếu \(h=15;\;a=16\) thì ta có:
\(OI=16:2=8\)
\( \Rightarrow l = \sqrt {{{15}^2} + {8^2}} = 17\)
\({S_{xq}} = 2.17.16 = 544\)
+) Nếu \(l=15;\;a=12\) thì ta có:
\(OI=12:2=6\)
\( \Rightarrow h = \sqrt {{{15}^2} - {6^2}} = \sqrt {189} \)
\({S_{xq}} = 2.15.12 = 360\)
+) Nếu \(a=10;\;S_{xq}=120\) thì ta có:
\( \Rightarrow l = \dfrac{{{S_{xq}}}}{{2a}} = \dfrac{{120}}{{2.10}} = 6\)
\(OI=10:2=5\)
\( \Rightarrow h = \sqrt {{6^2} - {5^2}} = \sqrt {11} \)
Ta điền vào bảng như sau:
|
Chiều cao \((h)\)
|
8
|
15
|
\(\sqrt {189} \)
|
\(\sqrt {11} \)
|
|
Trung đoạn \((l)\)
|
10
|
17
|
15
|
6
|
|
Cạnh đáy \((a)\)
|
12
|
16
|
12
|
10
|
|
\({S_{xq}}\)
|
240
|
544
|
360
|
120
|