Trên đường thẳng \(a\) lấy hai điểm \(I, B.\) Trên tia đối tia \(IB\) lấy điểm \(C\) sao cho \(IC = IB,\) trên tia đối tia \(BI\) lấy điểm \(D\) sao cho \(BD = BI.\) Ta có \(I\) là trung điểm của đoạn \(BC ;\) \(B\) là trung điểm của đoạn \(ID.\)
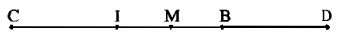
a) Ta có:
Vì \(I\) là trung điểm của đoạn \(CB\) nên \(\displaystyle IB = {{CB} \over 2}\) hay \(CB = 2IB\)
Vì \(B\) nằm giữa \(C\) và \(D\) nên \(CB + BD = CD\)
Mà \(BD = IB\) (do \(B\) là trung điểm đoạn \(ID)\) nên \(CD = 2IB +IB \)\(= 3IB\)
Vậy \(CD=3IB.\)
b) Vì điểm \(M\) là trung điểm của đoạn \(IB\) nên \(\displaystyle MI = MB = {{IB} \over 2}\)
Ta có \(B\) nằm giữa \(I\) và \(D\) mà \(M\) nằm giữa \(I\) và \(B\) nên điểm \(B\) nằm giữa hai điểm \(M\) và \(D\). Do đó \(MD = MB + BD\) (1)
Lại có \(I\) nằm giữa \(C\) và \(B\) mà \(M\) nằm giữa \(I\) và \(B\) nên điểm \(I\) nằm giữa hai điểm \(M\) và \(C\). Do đó \(MC = MI + IC.\) (2)
Từ (1) và (2) ta có \(MD = MB + BD\) và \(MC = MI + IC. \) Mà \(MI = MB;\)\( IC = BD\) nên \(MD=MI+IC= MC\)
Hay \(MD=MC\) (3)
Lại có \(M\) nằm giữa \(I \) và \(B\) nên \(M\) nằm giữa \(C\) và \(D. \) (4)
Từ (3) và (4) suy ra \(M\) là trung điểm của đoạn thẳng \(CD.\)