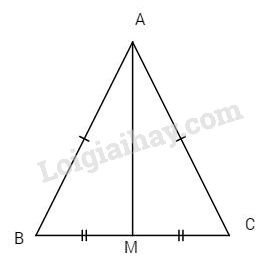
Xét \(\Delta ABM\) và \(\Delta ACM\) có
+) AM là cạnh chung
+) \(AM = MC\) (giả thiết)
+) \(AB = AC\) (giả thiết)
Do đó \(\Delta ABM = \Delta ACM\) (c.c.c)
\(AM \bot BC\) \( \Rightarrow \widehat {AMB} = \widehat {AMC}\) (góc tương ứng)
Mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\) (cặp góc kề bù)
Do đó \(\widehat {AMB} = \widehat {AMC} = {90^o}.\)
Chứng tỏ \(AM \bot BC.\)