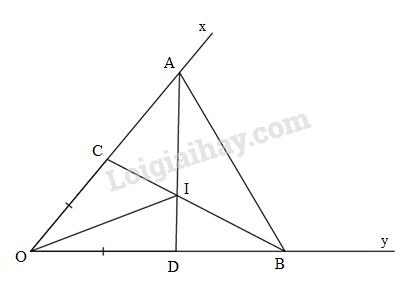
a) Xét \(\Delta ADO\) và \(\Delta BCO\) có:
+) OA = OB (giả thiết)
+) \(\widehat O\) chung
+) OD = OC (giả thiết)
Do đó \(\Delta ADO=\Delta BCO\) (c.g.c)
\( \Rightarrow AD = BC\) (cạnh tương ứng)
Và \(\widehat {ADO} = \widehat {BCO}\) (góc tương ứng).
Mà \(\widehat {ADO} + \widehat {ADB} = {180^o}\) (cặp góc kề bù) và \(\widehat {BCO} + \widehat {BCA} = {180^o}\)
\(\Rightarrow \widehat {ADB} = \widehat {BCA}.\)
Lại có \(OA = OB;\,OC = OD \)
\(\Rightarrow OA - OC = OB - OD\) hay \(AC = BD.\)
Xét \(\Delta ABC\) và \(\Delta BAD\) có:
+) AC = BD (chứng minh trên);
+) \(\widehat {ACB} = \widehat {BDA}\)(chứng minh trên);
+) AD = BC (chứng minh trên).
Do đó: \(\Delta ABC=\Delta BAD\) (c.g.c)
b) Xét \(\Delta OIA\) và \(\Delta OIB\) có:
+) OI chung,
+) IA = IB (giả thiết),
+) OA = OB (giả thiết)
Do đó \(\Delta OIA=\Delta OIB\) (c.c.c)
\( \Rightarrow \widehat {IOA} = \widehat {IOB}\).
Chứng tỏ OI là phân giác của \(\widehat {xOy}\)