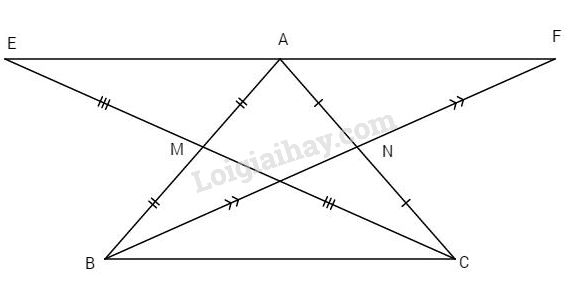
Xét \(\Delta AME\) và \(\Delta BMC\) có
+) \(MA = MB\) (giả thiết)
+) \(\widehat {AME} = \widehat {BMC}\) (đối đỉnh)
+) \(ME = MC\) (giả thiết)
Do đó \(\Delta AME=\Delta BMC\) (c.g.c)
\( \Rightarrow \widehat {EAB} = \widehat {CBM}\) (góc tương ứng)
Và \(AE = BC\) (cạnh tương ứng).
Hai góc \(\widehat {EAB}\) và \(\widehat {CBM}\) ở vị trí so le trong và \(\widehat {EAB} = \widehat {CBM}\) (chứng minh trên) \(\Rightarrow AE//BC\) (1).
Chứng minh tương tự ta có \(AE = AF\left( { = BC} \right)\) \(AF = BC\) và \(AF//BC\) (2).
Từ (1) và (2) \( \Rightarrow \) AE và AF phải trùng nhau (tiên đề Oclit) hay ba điểm E, A, F thẳng hàng và \(AE = AF\left( { = BC} \right)\).
Chứng tỏ A là trung điểm của EF.