Bài 1
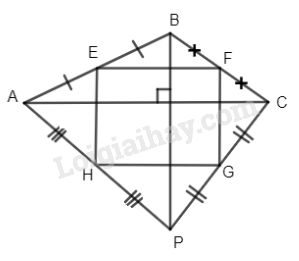
Ta có EF, HG lần lượt là các đường trung bình của \(\Delta ABC\) và \(\Delta ADC\) nên \({\rm{EF}}//HG//AC\) và EF = HG. Do đó tứ giác EFGH là hình bình hành.
Tương tự \(EH// BD\)mà \(BD \bot AC\left( {gt} \right) \Rightarrow {\rm{EF}} \bot {\rm{EH,}}\) do đó EFGH là hình chữ nhật và \(EF = {1 \over 2}AC = 4(cm),\) \(EH = {1 \over 2}BD = 3cm.\)
Vậy \({S_{EFGH}} = EF.EH = 12\left( {c{m^2}} \right).\)
Bài 2
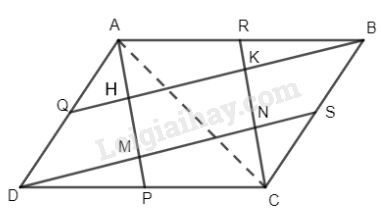
Nối A với C ta có AP là đường trung tuyến của \(\Delta ACD\) nên
\({S_{ADP}} = {S_{APC}} = {1 \over 2}{S_{ADC}} = {1 \over 4}{S_{ABCD}}\)
Tương tự \({S_{ACR}} = {S_{BCR}} = {1 \over 2}{S_{ABC}} = {1 \over 4}{S_{ABCD}}.\)
\( \Rightarrow {S_{APC}} + {S_{ACR}} = {S_{{\rm{AR}}CP}} = {1 \over 2}{S_{ABCD}}.\)
\({S_{ADP}} = {S_{APC}} = {1 \over 2}{S_{ADC}} = {1 \over 4}{S_{ABCD}}\)
Tương tự \({S_{ACR}} = {S_{BCR}} = {1 \over 2}{S_{ABC}} = {1 \over 4}{S_{ABCD}}.\)
\( \Rightarrow {S_{APC}} + {S_{ACR}} = {S_{{\rm{AR}}CP}} = {1 \over 2}{S_{ABCD}}.\)
Gọi H là giao điểm của AP và BQ, K là giao điểm của CR và BQ, M là giao điểm của AP và DS, N là giao điểm của CR và DS.
Dễ thấy HKNM là hình bình hành nên các tam giác sau đây có cùng diện tích:
\({S_{AKH}} = {S_{HKM}} = {S_{MNH}} = {S_{MNC}} \)\(\,= {S_{AKB}} = {S_{MCD}}\)
Mà \({S_{AKR}} = {1 \over 2}{S_{AKB}}\) (đáy gấp đôi, chung đường cao)
Tương tự \({S_{MPC}} = {1 \over 2}{S_{MCD}}\)
\( \Rightarrow {S_{AKH}} = {S_{HKM}} = {S_{MNH}} \)\(\,= {S_{MNC}} = \left( {{S_{AKR}} + {S_{MPC}}} \right) \)\(\,= {1 \over 5}{S_{ARCP}}.\)
Mà \({S_{ARCP}} = {1 \over 2}{S_{ABCD}}\)
\( \Rightarrow {S_{HKM}} + {S_{MKN}} = {1 \over 5}{S_{ABCD}}\) hay \({S_{KHMN}} = {1 \over 5}{S_{ABCD}}.\)