LG câu a
Phương pháp:
Lấy một điểm thuộc \(d\), chẳng hạn \(M=(0;1)\).
Khi đó \(M’=T_{\vec v}(M)\)
\(=(0-2;1+1)=(-2;2) \in d’\).
Vì \(d’\) song song với \(d\) nên phương trình của nó có dạng \(2x-3y+C=0\).
Do \(M’\in d’\) nên \(2.(-2)-3.2+C=0\) từ đó suy ra \(C=10\).
Do đó \(d’\) có phương trình \(2x-3y+10=0\).
LG câu b
Phương pháp:
Tính chất của phép tịnh tiến: Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với đường thẳng ban đầu.
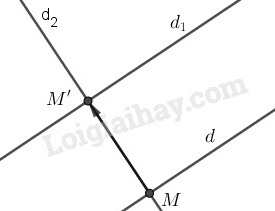
Ta có \(d_1=T_{\vec w}(d)\), nên \(\vec w\) có điểm đầu thuộc \(d\) điểm cuối thuộc \(d_1\).
Mục tiêu là viết phương trình đường thẳng \(d_2\) đi qua 2 điểm đầu, cuối đó.
Tìm giao của \(d_2\) với \(d\) và \(d_1\).
Lấy một điểm thuộc \(d\), chẳng hạn \(M=(0;1)\). Gọi đường thẳng \(d_2\) qua \(M\) vuông góc với \(d\) khi đó \(d_2\) có vectơ chỉ phương là \(\vec v=(2;-3)\). Do đó phương trình của \(d_2\) là \(\dfrac{x-0}{2}=\dfrac{y-1}{-3}\) hay \(3x+2y-2=0\). Gọi \(M’\) là giao của \(d_1\) với \(d_2\) thì tọa độ của nó phải thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}2x - 3y - 5 = 0\\3x + 2y - 2 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{{16}}{{13}}\\y = - \dfrac{{11}}{{13}}\end{array} \right.\)
Từ đó suy ra \(\overrightarrow {\rm{w}} = \overrightarrow {MM'} = \left( {\dfrac{{16}}{{13}}; - \dfrac{{24}}{{13}}} \right)\).