Trước hết ta thu gọn các đơn thức đồng dạng để xác định mỗi chữ cái tương ứng với kết quả nào trong ô trống của bảng.
V \(2{x^2} + 3{x^2} - \dfrac{1}{2}{x^2} = \left( {2 + 3 - \dfrac{1}{2}} \right){x^2} \)\(\,= \left( {\dfrac{4}{2} + \dfrac{6}{2} - \dfrac{1}{2}} \right){x^2} = \dfrac{9}{2}{x^2}\)
N \( - \dfrac{1}{2}{x^2} + {x^2} = \left( { - \dfrac{1}{2} + 1} \right){x^2} \)\(\,= \left( { - \dfrac{1}{2} + \dfrac{2}{2}} \right){x^2} = \dfrac{1}{2}{x^2}\)
H \(xy - 3xy + 5xy = \left( {1 - 3 + 5} \right)xy\)\(\, = 3xy\);
Ă \(7{y^2}{z^3} + ( - 7{y^2}{z^3}) = \left[ {7 + \left( { - 7} \right)} \right]{y^2}{z^3} \)\(\,= 0\);
Ư \(5xy - \dfrac{1}{3}xy + xy = \left( {5 - \dfrac{1}{3} + 1} \right)xy\)\(\, = \left( {\dfrac{{15}}{3} - \dfrac{1}{3} + \dfrac{3}{3}} \right)xy = \dfrac{{17}}{3}xy\)
U \( - 6{x^2}y - 6{x^2}y = \left[ {\left( { - 6} \right) - 6} \right]{x^2}y \)\(\,= - 12{x^2}y\)
Ê \(3x{y^2} - ( - 3x{y^2}) = 3x{y^2} + 3x{y^2} \)\(\,= \left( {3 + 3} \right)x{y^2} = 6x{y^2}\)
L \( - \dfrac{1}{5}{x^2} + \left( { - \dfrac{1}{5}{x^2}} \right) \)\(\,= \left[ {\left( { - \dfrac{1}{5}} \right) + \left( { - \dfrac{1}{5}} \right)} \right]{x^2}\)\(\, = \dfrac{{ - 2}}{5}{x^2}\)
Ta có bảng kết quả sau:
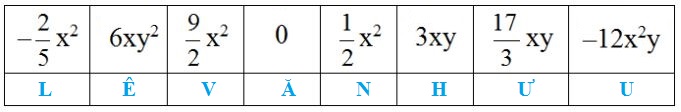
Vậy tên của tác giả cuốn Đại Việt sử kí là Lê Văn Hưu.