Ôn tập chương IV: Biểu thức đại số

Đề bài

Tính giá trị mỗi biểu thức sau tại \(x = 1; y = -1\) và \(z =- 2\).

a) \(2xy(5{x^2}y + 3x-z)\);

b) \(x{y^2} + {y^2}{z^3} + {z^3}{x^4}\).

Đề bài

Có hai vòi nước: vòi thứ nhất chảy vào bể \(A\), vòi thứ hai chảy vào bể \(B\). Bể \(A\) đã có sẵn \(100\) lít nước. Bể \(B\) chưa có nước. Mỗi phút vòi thứ nhất chảy được \(30\) lít, vòi thứ hai chảy được \(40\) lít.

a) Tính lượng nước có trong mỗi bể sau thời gian \(1, 2, 3, 4, 10\) phút rồi điền kết quả vào bảng sau (giả thiết bể đủ lớn để chứa nước):

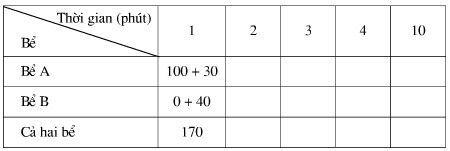
b) Viết biểu thức đại số biểu thị số lít nước trong mỗi bể sau thời gian \(x\) phút.

Đề bài

Tính tích các đơn thức sau rồi tìm hệ số và bậc của tích tìm được.

a) \(\dfrac{1}{4}x{y^3}\) và \(- 2{x^2}y{z^2}\)

b) \( - 2{x^2}yz\) và \( - 3x{y^3}z\)

Đề bài

Cho hai đa thức:

\(P\left( x \right) = {x^5} - 3{x^2} + 7{x^4} - 9{x^3} + {x^2} \)\(- \dfrac{1}{4}x\)

\(Q\left( x \right) = 5{x^4} - {x^5} + {x^2} - 2{x^3} + 3{x^2}\)\( - \dfrac{1}{4}\)

a) Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến.

b) Tính \(P(x) + Q(x)\) và \(P(x) - Q(x)\).

c) Chứng tỏ rằng \(x = 0\) là nghiệm của đa thức \(P(x)\) nhưng không phải là nghiệm của đa thức \(Q(x)\).

Đề bài

Cho đa thức: \(M(x) = 5{{\rm{x}}^3} + 2{{\rm{x}}^4} - {x^2} + 3{{\rm{x}}^2} - {x^3}\)\( - {x^4} + 1 - 4{{\rm{x}}^3}\)

a) Sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.

b) Tính \(M(1)\) và \(M(-1)\)

c) Chứng tỏ rằng đa thức trên không có nghiệm.

Đề bài

Trong các số cho bên phải mỗi đa thức, số nào là nghiệm của đa thức đó?

Đề bài

Bài 1: Cho \(f(x) = 9 - {x^5} + 4{\rm{x}} - 2{{\rm{x}}^3} + {x^2} - 7{{\rm{x}}^4};\)

        \(g(x) = {x^5} - 9 + 2{{\rm{x}}^2} + 7{{\rm{x}}^4} + 2{{\rm{x}}^3} - 3{\rm{x}}\).

a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến.

b) Tính tổng \(h(x) = f(x) + g(x)\).

c) Tìm nghiệm của đa thức h(x).

Bài 2: Cho \(A(x) = 6{{\rm{x}}^3} + 5{{\rm{x}}^2};B(x) = {x^3} - {x^2};\)\(\;C(x) =  - 2{{\rm{x}}^3} + 4{{\rm{x}}^2}.\)

a) Tìm \(D(x) = A(x) + B(x) - C(x)\).

b) Tìm nghiệm của đa thức D(x).

Bài 3: Tìm m để \(x =  - 1\) là nghiệm của đa thức \(M(x) = {x^2} - m{\rm{x}} + 2\).

Bài 4: Cho đa thức \(K(x) = a + b(x - 1) + c(x - 1)(x - 2)\) Tìm a, b, c biết \(K(1) = 1;K(2) = 3;K(0) = 5.\) 

Đề bài

Bài 1: Cho các đa thức:

\(f(x) = {x^3} - 2{{\rm{x}}^2} + 3{\rm{x}} + 1;g(x) = {x^3} + x - 1;h(x) = 2{{\rm{x}}^2} - 1.\)

a) Tính \(f(x) - g(x) + h(x).\)

b) Tìm x sao cho \(f(x) - g(x) + h(x) = 0.\)

Bài 2: Thu gọn và tính giá trị biểu thức: \(({4^2} - 2{\rm{x}} + 1) - ({x^2} - 4{\rm{x}} - 3),\) tại \(x =  - 2.\)

Bài 3: Cho đa thức \(E(x) = {x^2} + p{\rm{x}} + q.\) Tìm p, q biết \(x = 0\) và \(x =  - 1\) là hai nghiệm của \(E(x).\)  

Bài 4: Thu gọn biểu thức:

a) \(P = (5{\rm{x}} - 2) - (3{\rm{x}} - 3y);\)

b) \(Q = (8{{\rm{a}}^2} - 7{\rm{a}}b - {b^2}) + ( - 6{{\rm{a}}^2} + ab - 2{b^2}) - ( - {a^2} + 8{\rm{a}}b + 4{b^2}).\)

Bài 5: a) Tìm nghiệm của đa thức \(2{{\rm{x}}^2} + 3{\rm{x}} = 0\).

b) Cho \(A(x) = 2{{\rm{x}}^2} - 2{\rm{x}} - 24;\) \(B(x) = 2{{\rm{x}}^2} + 3{\rm{x}} - 29.\) Tìm x sao cho \(A(x) = B(x).\) 

Đề bài

Bài 1: Cho hai đa thức: \(A = 7{{\rm{a}}^2} - 4{\rm{a}}b - {b^2};B = 2{{\rm{a}}^2} - ab + {b^2}.\)

a) Tính \(A + B\).

b)  Tính \(A - B\).

Bài 2: Tìm nghiệm của đa thức:

a) \(5{\rm{x}} + 3(3{\rm{x}} + 7) - 35.\)

b) \({x^2} + 8{\rm{x}} - ({x^2} + 7{\rm{x}} + 8) - 9.\)  

Bài 3: Tìm m để \(x =  - 1\) là nghiệm của đa thức \(P(x) = {x^2} + 2{\rm{x}} + m - 1\).

Bài 4: Tìm đa thức M, biết: \(2({x^2} - 2{\rm{x}}y) - M = 6{{\rm{x}}^2} + 5{\rm{x}}y - {y^2}.\)

Bài 5: Cho hai đa thức: \(f(x) = {x^3} + 4{{\rm{x}}^2} - 3{\rm{x}} + 2;\)\(\;g(x) = {x^2}(x + 4) + x - 5.\) Tìm x sao cho \(f(x) = g(x).\) 

Đề bài

Bài 1: Cho hai đa thức: \(P =  - 2{{\rm{x}}^3} + x{y^2} + 3{\rm{x}};Q = 3{{\rm{x}}^3} - x{y^2} + 4{\rm{x}}.\)

a) Tính \(P + Q\).

b)  Tính \(P - Q\).

Bài 2: Cho hai đa thức: \(f(x) = {x^3} + {x^2} + x + 1;\)\(\;g(x) = {x^3} - 2{x^2} + x + 4\).

a) Chứng tỏ \(x =  - 1\) là nghiệm của f(x) và g(x).

b) Tính \(f(x) - g(x)\) và tìm giá trị của \(f(x) - g(x)\) tại \(x =  - {1 \over 2}.\)   

Bài 3: Tìm m để đa thức \(K(x) = m{{\rm{x}}^2} - 2{\rm{x}} + 4\) có một nghiệm là \(x =  - 2.\)

Bài 4: Tìm nghiệm của đa thức  \(M(x) = 2{{\rm{x}}^4} - 4{{\rm{x}}^3}\).

Bài 5: Cho \(A(x) = m + n{\rm{x}} + p{\rm{x}}(x - 1),\) biết \(A(0) = 5;A(1) =  - 2;A(2) = 7.\) Tìm đa thức A(x).

Đề bài

Bài 1: Cho \(A = 2{{\rm{a}}^2} + ab - {b^2} - ( - {a^2} + {b^2} - ab);\)

                 \(B = 3{{\rm{a}}^2} + {b^2} - (ab - {a^2})\).

a) Tính \(A + B\).

b) Tính \(A - B\).  

Bài 2: Cho:

  \(\eqalign{  & f(x) = {x^2}(2{x^3} - 3{x^2} + 5) - 6;  \cr  & g(x) = 3{x^5} - 2{x^4} + 3({x^3} + 1);  \cr  & h(x) = {x^5} + 2{x^3} - 7x + 4 \cr} \)

Tính \(f(x) + g(x) - h(x)\) và tính giá trị của  \(f(x) + g(x) - h(x)\) tại \(x =  - 1\).

Bài 3: Cho đa thức \(M(x) = {x^2} - 2m{\rm{x}} + m - 2\).

a) Tìm m biết \(M(1) =  - 3;\) 

b) Tìm nghiệm của M(x) với m vừa tìm được ở câu a)

Bài 4: Cho đa thức \(K(x) = {x^2} - 3{\rm{x}} + 2\) và \(L(x) = {x^2} + p{\rm{x}} + q + 1\).

Tìm p, q sao cho \(K(x) = L(x)\), với mọi giá trị của x.

Bài 5: Tìm nghiệm của đa thức \(M(x) =  - 3{{\rm{x}}^2} + 6{\rm{x}} - 4 - ( - 2{{\rm{x}}^2} + 5{\rm{x}} - 4)\).

Đề bài

Bài 1: Thu gọn hệ số và bậc của đơn thức:

a) \( - 2{1 \over 5}x{y^3}\left( {{{ - 25} \over {11}}{x^3}{y^2}} \right)\);

b) \({\left( { - {4 \over 5}{x^2}{y^5}} \right)^2}{\left( {{5 \over 2}{x^4}y} \right)^3}.\)

Bài 2: Cho đa thức: \(A(x) = 2{x^2} - 5x + 5;\)\(\;B(x) = 2{x^2} - 3x - 5\).

a) Tính \(A(x) - B(x)\).

b) Tính \(B( - 1)\). 

Bài 3: Cho đa thức \(A(x) = m{{\rm{x}}^2} + 2m{\rm{x}} - 3\). Tìm m để A(x) có nghiệm \(x =  - 1\).

Bài 4: Tìm nghiệm của các đa thức sau:

a) \(9{{\rm{x}}^2} - 1\).

b) \(8{{\rm{x}}^3} - 2{\rm{x}}\).

c) \((2{\rm{x}} + 3).(5 - x)\).