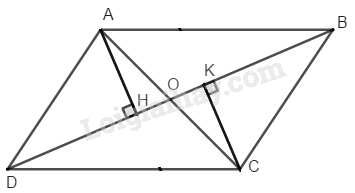
Xét \(∆ ABC\) và \(∆ CDA\) có:
\(AC\) chung
\(AB = CD\) (Vì \(ABCD\) là hình bình hành)
\(BC = DA\) (Vì \(ABCD\) là hình bình hành)
Suy ra \(∆ ABC = ∆ CDA \,(c.c.c)\)
\( \Rightarrow {S_{ABC}} = {S_{CDA}}\) \((1)\)
\(ABCD\) là hình bình hành nên \(OA = OC\) (tính chất hình bình hành)
Xét hai tam giác vuông \(AOH\) và \(CKO\) có:
\(OA = OC\) (cmt)
\(\widehat {AOH} = \widehat {COK}\) (đối đỉnh)
\( \Rightarrow \Delta AOH = \Delta COK\) (cạnh huyền-góc nhọn)
\( \Rightarrow AH = CK\) (hai cạnh tương ứng)
Mặt khác: \(AH,\, CK\) cùng vuông góc với \(BD\) nên \(AH // CK\)
Tứ giác \(AHCK\) có \(AH = CK\) (cmt) và \(AH //CK\) (cmt) nên \(AHCK\) là hình bình hành.
Do đó: \(AK = CH\) (tính chất hình bình hành)
Xét \(∆ AHC\) và \(∆ CKA\) có:
\(AC\) chung
\(CH = AK\) (cmt)
\(AH = CK\) (cmt)
\( \Rightarrow \) \(∆ AHC = ∆ CKA \,(c.c.c)\)
\( \Rightarrow {S_{AHC}} = {S_{CKA}}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra:
\({S_{ABC}} + {S_{AHC}} = {S_{CDA}} + {S_{CKA}}\)
Hay \({S_{ABCH}} = {S_{ADCK}}\)