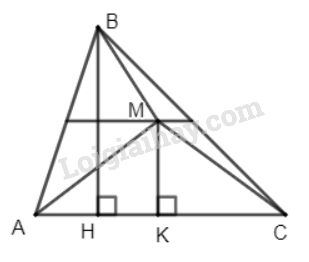
Kẻ đường cao \(BH, MK.\)
Theo giả thiết, \(M\) là điểm nằm trong tam giác \(ABC\) sao cho:
\({S_{AMB}} + {\rm{ }}{S_{BMC}} = {\rm{ }}{S_{MAC}}\) (1)
Ta lại có: \({S_{AMB}} + {S_{BMC}} + {S_{MAC}} = {S_{ABC}}\) (2)
Thay (1) vào (2) ta được: \({S_{MAC}}+ {S_{MAC}}={S_{ABC}}\)
Hay \({S_{MAC}} = \dfrac{1}{2}{S_{ABC}}\)
\(\Rightarrow \dfrac{1}{2}MK.AC = \dfrac{1}{2}\left( {\dfrac{1}{2}BH.AC} \right)\)
\(⇒MK = \dfrac{1}{2}BH\)
Do đó, \(M\) nằm trên đường thẳng sao cho khoảng cách từ \(M\) đến \(AC\) bằng \(\dfrac{1}{2}\) đường cao \(BH\).
Vậy điểm \(M\) nằm trong tam giác \(ABC\) và nằm trên đường trung bình ứng với cạnh \(AC\) của \(ΔABC\)