Bài 3. Đại lượng tỉ lệ nghịch

Đề bài

Cho biết \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch.

a) Thay các dấu "?" bằng các số thích hợp trong bảng dưới đây.

b) Có nhận xét gì về tích các giá trị tương ứng của \(x\) và \(y\) \(({x_1}{y_1},{x_2}{y_2},{x_3}{y_3},{x_4}{y_4})?\)

Đề bài

Cho biết \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch và khi \(x = 7\) thì \(y =10\).

a) Hãy tìm hệ số tỉ lệ nghịch của \(y\) đối với \(x\).

b) Hãy biểu diễn \(y\) theo \(x\).

c) Tính giá trị của \(y\) khi \(x = 5;  x = 14\).

Đề bài

Cho biết \(x\) và \(y\) là hai đại lương tỉ lệ nghịch. Điền các số thích hợp vào các ô trống trong bảng sau:

Đề bài

Một ô tô chạy từ A đến B với vận tốc \(45km/h\) hết \(3\) giờ \(15\) phút. Hỏi chiếc ô tô đó chạy từ A đến B với vận tốc \(65km/h\) sẽ hết bao nhiêu thời gian?

Đề bài

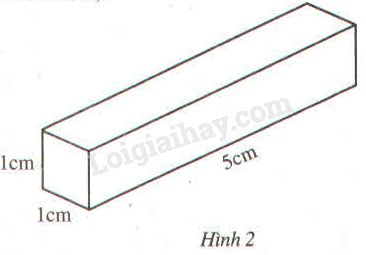
Đố: Một thỏi vàng hình hộp chữ nhật (hình dưới) có chiều dài 5cm, mặt cắt ngang (đáy) là một hình vuông cạnh 1cm. Từ thỏi vàng đó người ta làm thành một dây vàng cũng hình hộp chữ nhật. Đố em biết chiều dài của dây vàng đó bằng bao nhiêu nếu mặt cắt ngang của nó là hình vuông cạnh 1mm?

Bài 3.1

Tìm lỗi. Cho \(x\) tỉ lệ nghịch với \(y\) và \(y\) tỉ lệ nghịch với \( z\). Hãy cho biết mối quan hệ giữa \(x\) và \(z.\) Hãy nhận xét hai trả lời sau đây của hai bạn.

Bài giải của bạn Hùng:

\(\left\{ \begin{array}{l}x = \dfrac{y}{a}\left( {a \ne 0} \right)\\y = \dfrac{z}{b}\left( {b \ne 0} \right)\end{array} \right.\)\(\, \Rightarrow x = \dfrac{z}{b}:a = \dfrac{z}{{ab}}\left( {ba \ne 0} \right)\)

Vậy \(x\) tỉ lệ nghịch với \(z\) theo hệ số tỉ lệ \(b.a\).

Bài giải của bạn Hoa

\(\left\{ \begin{array}{l}x = \dfrac{a}{y}\left( {a \ne 0} \right)\\y = \dfrac{b}{z}\left( {b \ne 0} \right)\end{array} \right.\)\(\, \Rightarrow x = \dfrac{a}{{\dfrac{b}{z}}} = \dfrac{{a.z}}{b} = \dfrac{a}{b}.z\left( {\dfrac{a}{b} \ne 0} \right)\)

Vậy \(x\) tỉ lệ thuận với \(z\) theo hệ số tỉ lệ \(\dfrac{a}{b}.\)