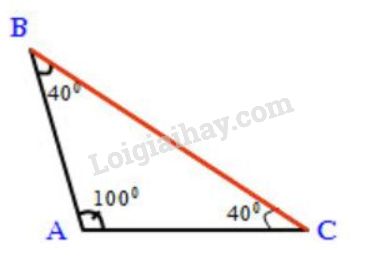
a) Tam giác \(ABC\) có \(\widehat{A} = 100^o\) \(\widehat{B} = 40^o\)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác \(ABC\) ta được:
\(\eqalign{
& \widehat A + \widehat B + \widehat C = {180^0} \cr
& \Rightarrow \widehat C = {180^0} - (\widehat A + \widehat B) \cr&\;\;\;\;\;\;\;\;\;= {180^0} - ({100^0} + {40^0}) = {40^0} \cr} \)
\( \Rightarrow \widehat A > \widehat B = \widehat C\) \(\left( {{{100}^o} > {{40}^o}} \right)\)
Vậy \(\widehat A\) lớn nhất do đó cạnh \(BC\) lớn nhất (Theo định lí về quan hệ giữa góc và cạnh đối diện)
b) Tam giác \(ABC\) có \(\widehat C = \widehat B = {40^0}\) do đó \(\Delta ABC \) là tam giác cân tại \(A\)