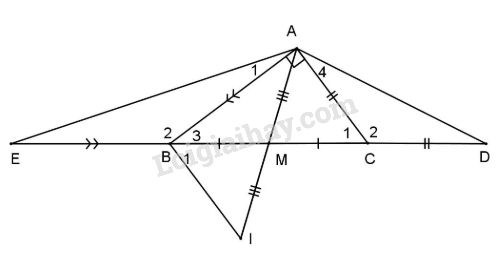
a) Dễ thấy \(\Delta AMC = \Delta IMB\) (c.g.c) \( \Rightarrow {\widehat C_1} = {\widehat B_1}\) (cặp góc so le trong bằng nhau)
\( \Rightarrow \) AC // BI , mà \(AC \bot AB\) (gt)
\( \Rightarrow AB \bot BI.\)
b) Ta có \(AB > AC \Rightarrow {\widehat C_1} > {\widehat B_3},\)
Mà \({\widehat C_1} + {\widehat C_2} = {180^0}\)
và \({\widehat B_2} + {\widehat B_3} = {180^0} \Rightarrow {\widehat C_2} < {\widehat B_2}\) (1)
Xét \(\Delta A{\rm{E}}B\) có \(AB = EB\) (gt) nên \(\Delta AEB\) cân tại B;
Tương tự \(\Delta AC{\rm{D}}\) cân tại C.
Suy ra \(\widehat E = {\widehat A_1} =\dfrac {{{{180}^0} - {{\widehat B}_2}} }{ 2}\)
và \(\widehat D = {\widehat A_4} =\dfrac {{{{180}^0} - {{\widehat C}_2}} }{2}\)
Mà theo (1) \( \Rightarrow \widehat E < \widehat D\). Do đó \(A{\rm{D}} < A{\rm{E}}.\)