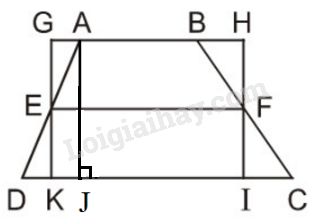
Ta có hình thang \(ABCD\) (\( AB// CD\)), với đường trung bình \(EF\) và hình chữ nhật \(GHIK\) như hình vẽ .
Xét hai tam giác vuông: \(∆AEG\) và \(∆DEK\) có:
+) \(AE = ED\) (do \(E\) là trung điểm của \(AD\))
+) \(\widehat {A{\rm{E}}G} = \widehat {DEK}\) (đối đỉnh)
\( \Rightarrow ∆AEG = ∆DEK\) (cạnh huyền-góc nhọn)
Tương tự \(∆BFH = ∆CFI\) (cạnh huyền-góc nhọn)
Do đó \({S_{ABCD}} = {S_{AEKIFB}} + {S_{DEK}} + {S_{CFI}} \)\(\,= {S_{AEKIFB}} + {S_{AEG}} + {S_{BFH}} = {S_{GHIK}}\)
Nên:
\({S_{ABCD}} = {S_{GHIK}} = EF.HI\) mà \(EF = \dfrac{{AB + CD}}{2}\)
Do đó \({S_{ABCD}} = \dfrac{{AB + CD}}{2}.HI\)
Gọi \(AJ\) là chiều cao của hình thang, từ đó suy ra:
\({S_{ABCD}} = \dfrac{{AB + CD}}{2}.AJ\) (do \(AJ = HI\))
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.