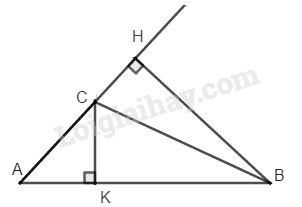
Trong tam giác \(ABC\) kẻ đường cao \(BH\) và \(CK\)
Ta có: \({S_{ABC}} = \dfrac {1}{2}AB.CK = \dfrac {1}{2}AC.BH\)
Suy ra: \(AB.CK = AC.BH\)
\( \Rightarrow \dfrac {BH}{CK} = \dfrac {AB}{AC}\)
Mà \(AB = 3 AC\) (gt) \( \Rightarrow \dfrac {BH}{CK} = \dfrac {3AC}{AC} = 3\)
Vậy đường cao \(BH\) dài gấp \(3\) lần đường cao \(CK.\)