Bài 3.1 phần bài tập bổ sung trang 160 SBT toán 8 tập 1

Đề bài

a) Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?

Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật.

b) Hãy chia một tam giác thành \(2\) phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó.

c) Hãy chia một tam giác thành \(4\) phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó.

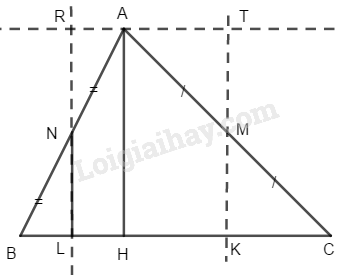
a) Xét \(∆ ABC.\) Kẻ đường cao \(AH.\) Gọi \(M\) là trung điểm của \(AC,\, N\) là trung điểm của \(AB.\)

Từ \(M\) kẻ đường thẳng song song \(AH\) cắt \(BC\) tại \(K\)

Từ \(N\) kẻ đường thẳng song song \(AH\) cắt \(BC\) tại \(L\)

Từ \(A\) kẻ đường thẳng song song \(BC\) cắt hai đường thẳng \(MK\) và \(NL\) tại \(T\) và \(R\)

Ta có: \(∆ MKC = ∆ MTA\)

\(∆ NLB = ∆ NAR\)

Cắt \(∆ ABC\) theo đường \(MK\) và \(NL\) ta ghép lại được một hình chữ nhật \(KTRL\) có diện tích bằng diện tích tam giác \(ABC\)

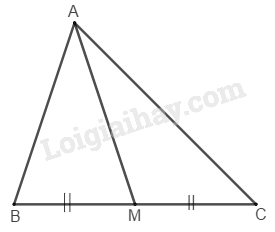
b) Ta đã biết hai tam giác có cạnh đáy bằng nhau và chung chiều cao thì có diện tích bằng nhau. Giả sử \(∆ ABC.\) Gọi \(M\) là trung điểm của \(BC\)

Cắt tam giác \(ABC\) theo đường \(AM\) chia tam giác \(ABC\) ra hai phần có diện tích bằng nhau.

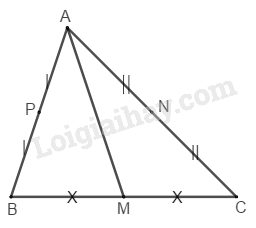
c) Tương tự như trên câu b.

Xét \(∆ ABC.\) Gọi \(M\) là trung điểm của \(BC\)

\(N\) là trung điểm của \(AC,\, P\) là trung điểm của \(AB\)

Cắt tam giác \(ABC\) theo đường \(AM\) ta có hai phần có diện tích bằng nhau

Cắt tam giác \(AMC\) theo đường \(AN\) ta có hai phần có diện tích bằng nhau

Cắt tam giác \(AMB\) theo đường \(MP\) ta có hai phần diện tích bằng nhau, ta có diện tích bốn phần chia bằng nhau.