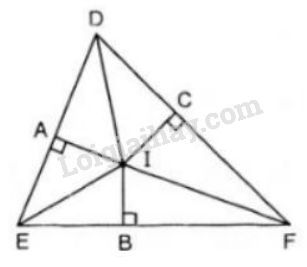
Từ điểm \(I\) ta kẻ \(IA ⊥ DE; IB ⊥ EF\) và \(IC ⊥ DF.\)
- Vì điểm \(I\) cách đều hai cạnh \(DE\) và \(DF\) nên \(I\) nằm trên đường phân giác của góc \(EDF\) (định lí 2 - định lí đảo của tia phân giác một góc)
- Vì điểm \(I\) cách đều hai cạnh \(FD\) và \(FE\) nên \(I\) nằm trên đường phân giác của góc \(EFD\) (định lí 2 - định lí đảo của tia phân giác một góc)
- Vì điểm \(I\) cách đều hai cạnh \(EF\) và \(ED\) nên \(I\) nằm trên đường phân giác của góc \(DEF\) (định lí 2 - định lí đảo của tia phân giác một góc)
Vậy \(I\) là điểm chung của ba đường phân giác của tam giác \(DEF.\)