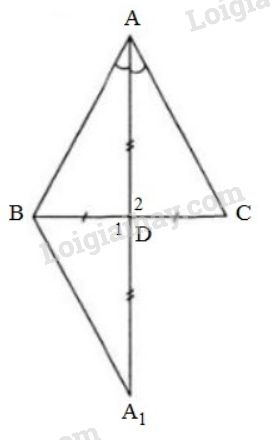
Gọi \(AD\) là đường trung tuyến đồng thời là đường phân giác của góc \(A\) trong \(ΔABC.\) Ta chứng minh \(∆ABC\) cân tại \(A.\)
Kéo dài \(AD\) một đoạn \(D{A_1}= AD.\)
Xét \(∆ADC\) và \(∆{A_1}DB\) ta có:
+) \(DC = DB\) (do \(AD\) là trung tuyến)
+) \({ \widehat{D}}_1 = {\widehat{D}}_2 \) (\(2\) góc đối đỉnh)
+) \(AD = D{A_1}\) (do cách vẽ)
Vậy \(∆ADC = ∆{A_1}DB\) (c.g.c)
\(\Rightarrow AC = {A_1}B\) (1)
và \(\widehat{DAC}= \widehat{DA_1B}\)
Mà \(\widehat{BAD}= \widehat{DAC}\) (Vì \(AD\) là phân giác)
\(\Rightarrow \) \(\widehat{BAD}=\widehat{DA_1B}\)
Xét tam giác \(AB{A_1}\) có \( \widehat{DA_1B} = \widehat{BAD}\)
Vậy \(AB{A_1}\) cân tại \(B\)
\(\Rightarrow AB = {A_1}B\) (2)
Từ (1) và (2) suy ra \(AB = AC\).
Vậy \(∆ABC\) cân tại \(A.\)
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.