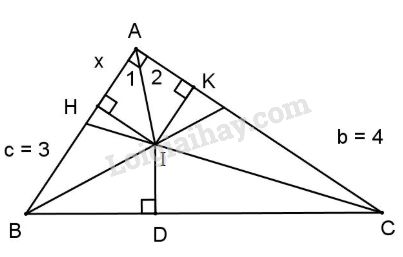
Cách 1:
Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{3^2} + {4^2}} = 5\) (cm) (định lý Pytago).
AI là phân giác của \(\widehat A\) \( \Rightarrow {\widehat A_1} = {\widehat A_2} = \dfrac{{\widehat A}}{2} = {45^0}.\)
Do đó \(\Delta AHI\) và \(\Delta AKI\) là các tam giác vuông cân \( \Rightarrow AH = IH\) và \(AK = IK.\)
Mặt khác vì I thuộc phân giác góc A nên \(IH = IK \Rightarrow IH = IK = AK = AH.\)
Kẻ \(I{\rm{D}} \bot BC\), ta cũng có \(I{\rm{D}} = IH\).
Gọi ba cạnh của tam giác ABC là a, b, c. Đặt \(AH = x\) ta có \(BH = B{\rm{D}} = c - x\);
Tương tự \(CK = C{\rm{D}} = b - x,\) mà \(a = B{\rm{D}} + C{\rm{D}}\) nên \(a = c - x + b - x \)
\(\Rightarrow x = \dfrac{{b + c - a} }{ 2} = \dfrac{{4 + 3 - 5} }{2} = 1\) (cm).
Vậy \(HI = I{\rm{D}} = IK = x = 1\) (cm).
Cách 2:
\(IH = IK = I{\rm{D}} = x;\)\(\;{S_{\Delta ABC}} = \dfrac{{AB.AC} }{ 2} = 6.\)
\(\eqalign{ {S_{\Delta ABC}} &= {S_{\Delta AIC}} + {S_{\Delta AIB}} + {S_{\Delta BIC}} \cr&= {1 \over 2}IK.AC + {1 \over 2}IA.AB \cr & {\rm{ }} = {x \over 2}(ac + ab + bc) = 6x \cr} \)
\(\Rightarrow x = 1. \)