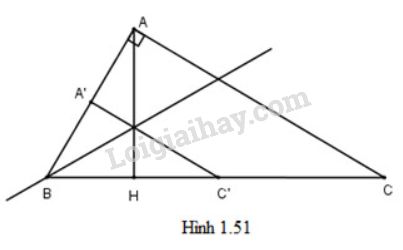
Gọi \(d\) là đường phân giác của \( \widehat{B}\). Gọi \(A' = {D_d}\left( H \right),C' = {D_d}\left( A \right)\)
Ta có \({D_{d}}\) biến \(∆HBA\) thành \(∆A'BC'\).
Lại có \(\frac{{BA}}{{BA'}} = \frac{{BC}}{{BC'}} = \frac{{AC}}{{A'C'}} = \frac{{AC}}{{AH}}=k\)
Nên \({V_{\left( {B;k} \right)}}\left( {A'} \right) = A,{V_{\left( {B;k} \right)}}\left( B \right) = B,\) \({V_{\left( {B;k} \right)}}\left( {C'} \right) = C\) hay \({V_{\left( {B;k} \right)}}\left( {\Delta A'BC'} \right) = ABC\).
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp \({D_{d}}\) và \({V_{(B,k)}}\) sẽ biến \( \bigtriangleup\)\(HBA\) thành \( \bigtriangleup\)\(ABC\)