PhươngPhương pháp:
Sử dụng: - CCông thức tính thể tích hình trụ: \(V= Sh = πr^2h\). (\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao, \(S\) là diện tích đáy
Sử dụng:
- Công thức tính thể tích hình trụ: \(V= Sh = πr^2h\).
(\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao, \(S\) l
Thể tích hình trụ có bán kính \(r\) và đường cao \(h\) có thể tích là: \(V = \pi {r^2}.h\)
- Nếu tăng gấp đôi bán kính thì thể tích trụ là \({V_1} = \pi {\left( {2r} \right)^2}h = 4\pi {r^2}h = 4V\).
- Nếu tăng gấp đôi chiều cao thì thể tích hình trụ là: \({V_2} = \pi {r^2}.2h = 2\pi {r^2}h = 2V\).
- Nếu tăng gấp đôi bán kính và chiều cao thì thể tích hình trụ là:
\({V_3} = \pi {\left( {2r} \right)^2}.2h = 8\pi {r^2}h = 8V\).
Vậy bạn Ngọc nói đúng.
Bài IV. 2
Quan sát hình trụ ở hình bs.30 rồi điền số thích hợp vào ô trống trong bảng sau (lấy \(\pi = 3,14\))
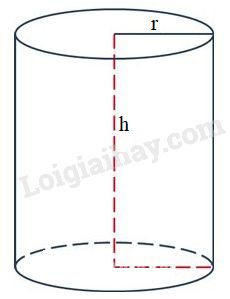
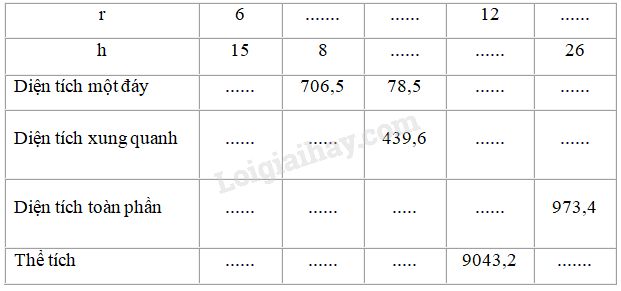
Phương pháp:
Sử dụng:
- Công thức tính diện tích xung quanh hình trụ: \({S_{xq}} = 2πrh\).
- Công thức tính diện tích toàn phần hình trụ: \({S_{tp}} = S_{xq} + 2S_đ = 2πrh + 2πr^2\).
- Công thức tính diện tích đáy hình trụ: \(S_{đ}= \pi r^2\) .
- Công thức tính thể tích hình trụ: \(V= Sh = πr^2h\).
(\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao).
* Hình trụ có \(r=6;h=15\)
Diện tích một đáy của hình trụ là: \({S_đ} = \pi {r^2} = \pi {.6^2} = 113,04\)
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh = 2\pi .6.15 = 565,2\)
Diện tích toàn phần của hình trụ là:
\({S_{TP}} = {S_{xq}} + 2{S_đ} = 565,2 + 2.113,04\)\(\, = 791,28\)
Thể tích của hình trụ là:
\(V = \pi {r^2}h = \pi {.6^2}.15 = 1695,6\)
* Hình trụ có \(h=8;S_đ=706,5\)
Ta có: \({S_đ} = \pi {r^2}\) \( \Rightarrow r = \sqrt {\dfrac{{{S_đ}}}{\pi }} = \sqrt {\dfrac{{706,5}}{{3,14}}} = 15\)
\({S_{xq}} = 2\pi rh = 2\pi .15.8 = 753,6\)
\({S_{TP}} = {S_{xq}} + 2{S_d} = 753,6 + 2.706,5\) \( = 2166,6\)
\(V = \pi {r^2}h = \pi {.15^2}.8 = 5652\)
* Hình trụ có \(S_đ=78,5;S_{xq}=439,6\)
\({S_đ} = \pi {r^2} \Rightarrow r = \sqrt {\dfrac{{{S_đ}}}{\pi }} = \sqrt {\dfrac{{78,5}}{{3,14}}} = 5\)
\({S_{xq}} = 2\pi rh \Rightarrow h = \dfrac{{{S_{xq}}}}{{2\pi r}} = \dfrac{{439,6}}{{2.3,14.5}} \)\(\,= 14\)
\({S_{TP}} = {S_{xq}} + 2{S_đ} = 439,6 + 2.78,5\)\(\, = 596,6\)
\(V = \pi {r^2}h = \pi {.5^2}.14 = 1099\)
* Hình trụ có \(r=12; V=9043,2\)
\(V = \pi {r^2}h\) \( \Rightarrow h = \dfrac{V}{{\pi {r^2}}} = \dfrac{{9043,2}}{{3,{{14.12}^2}}} = 20\)
\({S_đ} = \pi {r^2} = 3,{14.12^2} = 452,16\)
\({S_{xq}} = 2\pi rh = 2.3,14.12.20 = 1507,2\)
\({S_{TP}} = {S_{xq}} + 2{S_d} \)\(\,= 1507,2 + 2.452,16 \)\(\,= 2411,52\)
* Hình trụ có \(h=26;S_{TP}=973,4\)
\(\begin{array}{l}{S_{TP}} = 2\pi rh + 2\pi {r^2} = 973,4\\ \Rightarrow 2.3,14.r.26 + 2.3,14.{r^2} = 973,4\\ \Rightarrow {r^2} + 26r - 155 = 0\\ \Rightarrow \left[ \begin{array}{l}r = 5 \text{ (nhận)}\\r = - 31\text{ (loại)}\,\end{array} \right.\end{array}\)
\({S_đ} = \pi {r^2} = 3,{14.5^2} = 78,5\)
\({S_{xq}} = 2\pi rh = 2.3,14.5.26 = 816,4\)
\(V = \pi {r^2}h = 3,{14.5^2}.26 = 2041\)
Ta điền vào bảng như sau:
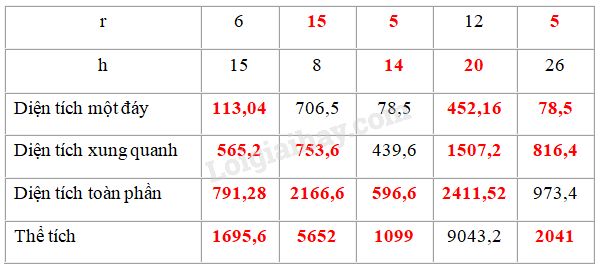
Bài IV.3
Thể tích của một hình nón thay đổi thế nào nếu:
a) Gấp đôi chiều cao của hình nón.
b) Gấp đôi bán kính của hình nón.
c) Gấp đôi cả chiều cao và bán kính đáy của hình nón.
Phương pháp:
Sử dụng:
- Công thức tính thể tích hình nón : \(\displaystyle V = {1 \over 3}\pi {r^2}h\).
(\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao).
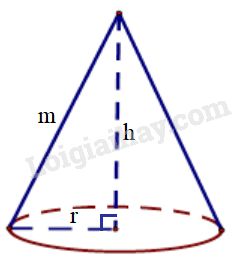
Hình nón có bán kính đáy \(r\), chiều cao \(h\), có thể tích là: \(\displaystyle V = {1 \over 3}\pi {r^2}h\).
a) Nếu gấp đôi chiều cao thì thể tích hình nón là:
\(\displaystyle {V_1} = {1 \over 3}\pi {r^2}.\left( {2h} \right) = 2.{1 \over 3}\pi {r^2}h = 2V\).
b) Nếu gấp đôi bán kính thì thể tích hình nón là:
\(\displaystyle {V_2} = {1 \over 3}\pi {\left( {2r} \right)^2}.h = 4.{1 \over 3}\pi {r^2}h = 4V\).
c) Nếu gấp đôi cả bán kính và chiều cao thì hình nón có thể tích là:
\(\displaystyle {V_3} = {1 \over 3}\pi {\left( {2r} \right)^2}.2h = 8.{1 \over 3}\pi {r^2}h = 8V\).