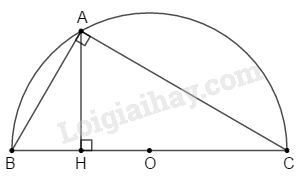
a) Đặt độ dài cạnh \(AB = x\); điều kiện \(x > 0\).
Theo điều kiện (1) ta có: \(BC = x + a\) (3)
Từ (2) và (3) \( \Rightarrow\displaystyle AC = {1 \over 2}\left( {x + 2a + x} \right) = x + a\)
Áp dụng định lí Pitago vào \(\Delta ABC\) vuông tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow {\left( {x + 2a} \right)^2} = {x^2} + {\left( {x + a} \right)^2}\)
\( \Rightarrow {x^2} + 4ax + 4{a^2} = {x^2} + {x^2} + 2ax \)\(\,+ {a^2} \)
\( \Rightarrow{x^2} - 2ax - 3{a^2} = 0 \)
\( \Delta = {\left( { - 2a} \right)^2} - 4.1\left( { - 3{a^2}} \right) \)\(\,= 4{a^2} + 12{a^2} = 16{a^2} > 0 \)
\(\Rightarrow \sqrt \Delta = \sqrt {16{a^2}} = 4a \)
\(\displaystyle {x_1} = {{2a + 4a} \over {2.1}} = {{6a} \over 2} = 3a \)
\(\displaystyle {x_2} = {{2a - 4a} \over {2.1}} = - a \)
Vì \(x > 0\) \( \Rightarrow {x_2} = - a\) (loại)
Vậy cạnh \(AB = 3a; AC = 3a + a = 4a;\) \(BC = 3a + 2a =5a\).
Ta có \(AH.BC = AB.AC\)
\( \displaystyle \Rightarrow AH = {{AB.AC} \over {BC}} = {{3a.4a} \over {5a}} \)\(\,\displaystyle = {{12a} \over 5}\)
b) Diện tích của \(\Delta ABC\) là:
\(\displaystyle {S_1} = {1 \over 2}AB.AC = {1 \over 2}.3a.4a = 6{a^2}\) (đơn vị diện tích)
\(\Delta ABC\) nội tiếp trong (O) bán kính đường tròn: \(\displaystyle R = {{BC} \over 2} = {{5a} \over 2}\)
Diện tích nửa hình tròn là: \(\displaystyle {S_2} = {1 \over 2}\pi .{r^2} = {1 \over 2}\pi .{\left( {{{5a} \over 2}} \right)^2} \)\(\,\displaystyle = {{25\pi {a^2}} \over 8}\)
Phần diện tích nửa hình tròn nằm ngoài tam giác là:
\(\displaystyle S = {S_2} - {S_1} = {{25\pi {a^2}} \over 8} - 6{a^2}\)\(\,\displaystyle = {{{a^2}} \over 8}\left( {25\pi - 48} \right)\)
c) Khi quay \(\Delta ABC\) một vòng quanh cạnh \(BC\) thì \(AB\) và \(AC\) vạch lên hai hình nón có bán kính đáy là \(AH.\)
Diện tích xung quanh hình nón do dây cung \(AB\) tạo ra là:
\(\displaystyle {S_1} = \pi .AH.AB = \pi .AH.3a\)
Diện tích xung quanh hình nón do dây cung cung \(AC\) tạo ra là:
\( {S_2} = \pi .AH.AC = \pi AH.4a \)
Tỉ số diện tích giữa các phần do các dây cung \(AB\) và \(AC\) tạo ra là:
\(\displaystyle {{{S_1}} \over {{S_2}}} = {{\pi .AH.3a} \over {\pi .AH.4a}} = {3 \over 4} \).