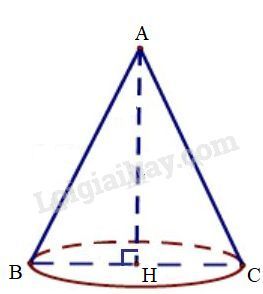
a) Áp dụng định lí Pytago vào tam giác vuông \(AHB\), ta có:
\( A{B^2} = A{H^2} + B{H^2}\)\(\, = 4{r^2} + {r^2} = 5{r^2} \)
\(\Rightarrow AB = r\sqrt 5 \).
Diện tích toàn phần hình nón:
\( {S_{TP}} = {S_{xq}} + {S _\text{đáy}}\)\(\, = \pi .r.r\sqrt 5 + \pi {r^2}\)\(\,= \pi {r^2}\left( {\sqrt 5 + 1} \right) \)
\( {S_{TP}} = 21,06 \)
\(\Rightarrow \pi {r^2}\left( {\sqrt 5 + 1} \right) = 21,06 \)
\( \displaystyle \Rightarrow {r^2} = {{21,06} \over {\pi \left( {\sqrt 5 + 1} \right)}} \)
Diện tích mặt cầu là:
\( S = 4\pi {r^2} \)
\(\displaystyle S = 4\pi .{{21,06} \over {\pi \left( {\sqrt 5 + 1} \right)}} \)\(\,\displaystyle= 21,06.\left( {\sqrt 5 - 1} \right) \approx 26,03\left( {c{m^2}} \right) \)
b) Thể tích hình cầu là: \(\displaystyle V = {4 \over 3}\pi {r^3}\)
Thể tích hình cầu bằng \(15,8c{m^3}\)
\(\displaystyle \Rightarrow {4 \over 3}\pi {r^3} = 15,8 \)
\(\displaystyle \Rightarrow {r^3} = {{47,4} \over {4\pi }} = {{23,7} \over {2\pi }}\)
Thể tích hình nón là:
\(\displaystyle V = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {r^2}.2r = {2 \over 3}\pi {r^3} \)
\(\displaystyle \Rightarrow V = {2 \over 3}\pi .{{23,7} \over {2\pi }} = {{23,7} \over 3} \)\(\,= 7,9\left( {c{m^3}} \right) \).