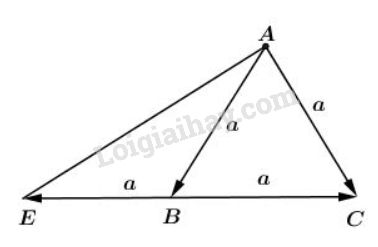
Ta có \(\overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}\)
\(\left | \overrightarrow{AB}+\overrightarrow{BC} \right | = \left | \overrightarrow{AC} \right |= a.\)
Ta có: \(\overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{AB} +\overrightarrow{CB}.\)
Trên tia \(CB,\) ta dựng \(\overrightarrow{BE} = \overrightarrow{CB}.\)
\( \Rightarrow \overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{AB} +\overrightarrow{BE}= \overrightarrow{AE}\)
Tam giác \(EAC\) vuông tại \(A\) (vì có đường trung tuyến \(AB\) bằng nửa cạnh \(CE\)) có : \(AC = a, \, \, CE = 2a,\) suy ra \(AE = \sqrt {C{E^2} - A{C^2}} = \sqrt {4{a^2} - {a^2}} \)\(= a\sqrt 3. \)
Vậy \(\left | \overrightarrow{AB } -\overrightarrow{BC}\right | = \left | \overrightarrow{AE} \right | = a\sqrt3.\)