a) TXĐ: \(D =\mathbb R\backslash \left\{ { - 2} \right\}\)
\(\mathop {\lim }\limits_{x \to - {2^ + }} y = + \infty ;\,\,\mathop {\lim }\limits_{x \to - {2^ - }} y = - \infty \) nên \(x = -2\) là tiệm cận đứng.
Ta có: \(y = 2x + 1 + {2 \over {x + 2}}\)
\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {2 \over {x + 2}} = 0\) nên \(y = 2x + 1\) là tiệm cận xiên
\(\eqalign{
& y' = 2 - {2 \over {{{\left( {x + 2} \right)}^2}}} = {{2\left[ {{{\left( {x + 2} \right)}^2} - 1} \right]} \over {{{\left( {x + 2} \right)}^2}}} = {{2\left( {x + 1} \right)\left( {x + 3} \right)} \over {{{\left( {x + 2} \right)}^2}}} \cr
& y' = 0 \Leftrightarrow \left[ \matrix{
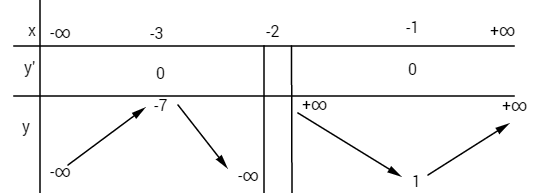
x = - 1;\,\,y\left( { - 1} \right) = 1 \hfill \cr
x = - 3;\,\,y\left( { - 3} \right) = - 7 \hfill \cr} \right. \cr} \)
Bảng biến thiên:
Điểm đặc biệt: \(x = 0 \Rightarrow y = 2\)
b) Giao điểm hai đường tiệm cận của đồ thị là nghiệm của hệ.
\(\left\{ \matrix{ x = - 2 \hfill \cr y = 2x + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 2 \hfill \cr y = - 3 \hfill \cr} \right.\)
Vậy \(I\left( { - 2; - 3} \right)\)
Công thức đổi trục tịnh tiến theo véc tơ \(\overrightarrow {OI} \) là
\(\left\{ \matrix{ x = X - 2 \hfill \cr y = Y - 3 \hfill \cr} \right.\)
Ta có:
\(\eqalign{
& Y - 3 = 2(X - 2) + 1 + {2 \over {X - 2 + 2}} \cr
& \Leftrightarrow Y - 3 = 2X - 4 + 1 + {2 \over X} \cr
& \Leftrightarrow Y = 2X + {2 \over X} \cr} \)
Hàm số là hàm số lẻ nên đồ thị của hàm số nhận gốc \(I\) làm tâm đối xứng.
c) Ta có: \({{2{x^2} + 5x + 4} \over {x + 2}} + m = 0 \Leftrightarrow {{2{x^2} + 5x + 4} \over {x + 2}} = - m\)
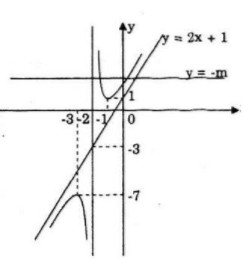
Số nghiệm của phương trình chính là số giao điểm của đồ thị \((C)\) hàm số và đường thẳng \(y = -m\).
Dựa vào đồ thị ta có:
+) \(- m< -7\) hoặc \(–m>1\) \( \Leftrightarrow m > 7\) hoặc \(m< -1\) : phương trình có \(2\) nghiệm;
+) \(-m=-7\) hoặc \(–m = 1 \Leftrightarrow m = 7\) hoặc \(m = -1\): phương trình có \(1\) nghiệm;
+) \(- 7<m< 1 \Leftrightarrow -1 < m < 7\): phương trình vô nghiệm.