a) Tập xác định: \(D = R\backslash \left\{ 1 \right\}\)
\(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D\)
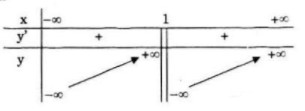
Vậy hàm số đồng biến trên khoảng \(( - \infty ;1)\) và \((1; + \infty )\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \cr
& \mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \cr} \)
Do đó \(x=1\) là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to \pm \infty } (y - x) = \mathop {\lim }\limits_{x \to \pm \infty } \left( { - {2 \over {x - 1}}} \right) = 0\)
Vậy \(y=x\) là tiệm cận xiên.
Bảng biến thiên:
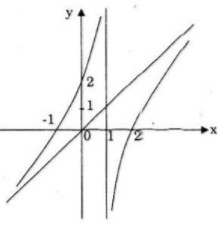
Đồ thị giao \(Ox\) tại \((-1;0),(2;0)\)
Đồ thị giao \(Oy\) tại \(0;2)\)
b) Ta có: \(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}}\)
Phương trình tiếp tuyến với đồ thị hàm số đã cho tại điểm \(M\left( {{x_o};{y_o}} \right) \in \left( C \right)\) là:
\(\left( d \right):\,y - {x_o} + {2 \over {{x_o} - 1}} = \left[ {1 + {2 \over {{{\left( {{x_o} - 1} \right)}^2}}}} \right]\left( {x - {x_o}} \right)\,\left( {x \ne 1} \right)\)
Vì \(\left( {3;3} \right) \in d\) nên \(3 - {x_o} + {2 \over {{x_o} - 1}} = {{{{\left( {{x_o} - 1} \right)}^2} + 2} \over {{{\left( {{x_o} - 1} \right)}^2}}}\left( {3 - {x_o}} \right)\)
\(\eqalign{
& \Leftrightarrow \left( {3 - {x_o}} \right){\left( {{x_o} - 1} \right)^2} + 2\left( {{x_o} - 1} \right) = \left( {{x_o} - 2{x_o} + 3} \right)\left( {3 - {x_o}} \right) \cr
& \Leftrightarrow {x_o} = 2;\,{y_o} = y\left( 2 \right) = 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y'\left( 2 \right) = 3 \cr} \)
Vậy phương trình tiếp tuyến cần tìm là: \(y = 3\left( {x - 2} \right)\) hay \(y = 3x - 6.\)