a) TXĐ: \(D =\mathbb R\backslash \left\{ 2 \right\}\)Tiệm cận đứng \(x = 2\); tiệm cận ngang \(y = 1\).
\(y' = {{ - 3} \over {{{\left( {x - 2} \right)}^2}}} < 0\) với mọi \(x \ne 2\)
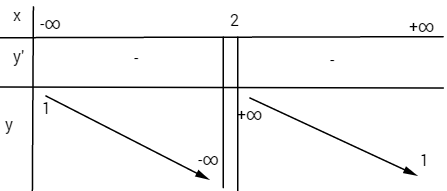
Điểm đặc biệt: \(A\left( {0; - {1 \over 2}} \right),\,B\left( { - 1;0} \right)\)
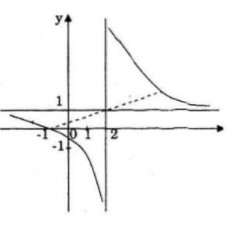
Đồ thị nhận điểm \(I(2;1)\) làm tâm đối xứng.
b) Giao điểm của đồ thị với trục tung \(A\left( {0; - {1 \over 2}} \right)\)
\(y'\left( 0 \right) = - {3 \over 4}\)
Phương trình tiếp tuyến của đồ thị tại \(A\) là:
\(y + {1 \over 2} = - {3 \over 4}\left( {x - 0} \right) \Leftrightarrow y = - {3 \over 4}x - {1 \over 2}\)
c) Giả sử \(M\) là tiếp điểm của tiếp tuyến song song với tiếp tuyến tại \(A\) ta có:
\(y'\left( {{x_M}} \right) = - {3 \over 4} \Leftrightarrow {{ - 3} \over {{{\left( {{x_M} - 2} \right)}^2}}} = - {3 \over 4} \Leftrightarrow {\left( {{x_M} - 2} \right)^2} = 4\)
\( \Leftrightarrow \left[ \matrix{ {x_M} - 2 = 2 \hfill \cr {x_M} - 2 = - 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ {x_M} = 4 \hfill \cr {x_M} = 0\,\,(\text{ loại vì }{x_A} = 0) \hfill \cr} \right.\)
\(y\left( 4 \right) = {5 \over 2}\). Vậy \(M\left( {4;{5 \over 2}} \right)\)
Phương trình tiếp tuyến tại điểm \(M\) là: \(y - {5 \over 2} = - {3 \over 4}\left( {x - 4} \right) \Leftrightarrow y = - {3 \over 4}x + {{11} \over 2}\)