Bài 52 trang 15 SBT toán 9 tập 2

Đề bài

Giải các hệ phương trình sau:

\(a)\left\{ {\matrix{
{\sqrt 3 x - 2\sqrt 2 y = 7} \cr 
{\sqrt 2 x + 3\sqrt 3 y = - 2\sqrt 6 } \cr} } \right.\)

\(b)\left\{ {\matrix{
{\left( {\sqrt 2 + 1} \right)x - \left( {2 - \sqrt 3 } \right)y = 2} \cr 
{\left( {2 + \sqrt 3 } \right)x + \left( {\sqrt 2 - 1} \right)y = 2} \cr} } \right.\)

\(a)\)

\(\eqalign{
& \left\{ {\matrix{
{\sqrt 3 x - 2\sqrt 2 y = 7} \cr 
{\sqrt 2 x + 3\sqrt 3 y = - 2\sqrt 6 } \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{\sqrt 6 x - 4y = 7\sqrt 2 } \cr 
{\sqrt 6 x + 9y = - 6\sqrt 2 } \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{13y = - 13\sqrt 2 } \cr 
{\sqrt 3 x - 2\sqrt 2 y = 7} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{y = - \sqrt 2 } \cr 
{\sqrt 3 x - 2\sqrt 2 .\left( { - \sqrt 2 } \right) = 7} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{y = - \sqrt 2 } \cr 
{\sqrt 3 x = 3} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{y = - \sqrt 2 } \cr 
{x = \sqrt 3 } \cr} } \right. \cr} \)

Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) = \left( {\sqrt 3 ; - \sqrt 2 } \right)\)

\(b)\)

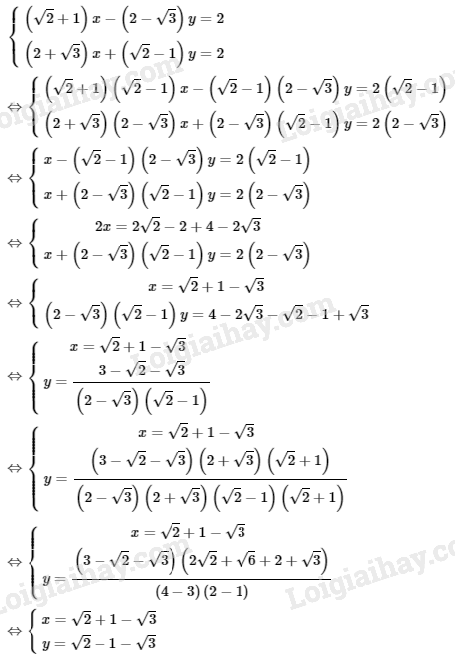
Vậy hệ phương trình đã cho có nghiệm duy nhất là \((x; y) =( {\sqrt 2  + 1 - \sqrt 3 ;\sqrt 2  - 1 - \sqrt 3 } )\)