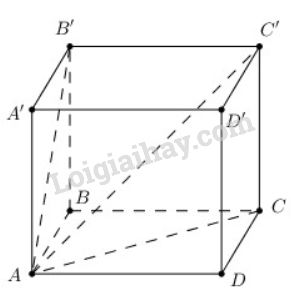
a) Ta có: \(DA ⊥ (ABB'A'), DA ⊂ (ADC'B')\)
\(\Rightarrow (ADC'B') \bot(ABB'A')\).
b) Xét tam giác vuông \(ACC'\))
\(AC' = \sqrt {A{C^2} + CC{'^2}} = \sqrt {A{D^2} + D{C^2} + CC{'^2}}\)
\(=\sqrt{a^{2}+b^{2}+c^{2}}.\)
Ghi nhớ: Hai mặt phẳng vuông góc với nhau khi mặt này chứa một đường thẳng vuông góc với mặt kia.