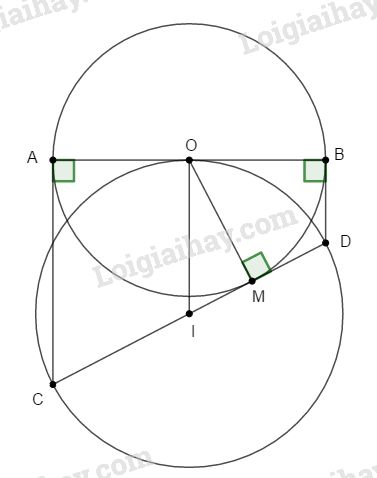
AC và BD là tiếp tuyến của (O) nên \(AC ⊥ AB\) và \(BD ⊥ AB ⇒ AC // BD\)
Do đó tứ giác ACDB là hình thang vuông, có O là trung điểm AB, I là trung điểm CD nên OI là đường trung bình của hình thang vuông. Vì vậy OI // AC.
\(⇒ OI ⊥ AB\) (1) và \(OI = {{AC + BD} \over 2}\)
Dễ dàng chứng minh \(∆OAC = ∆OMC ⇒ AC = MC\)
Tương tự : \(BD = MD \)\(\;\Rightarrow OI = {{MC + MD} \over 2} = {{CD} \over 2}\,\left( 2 \right)\)
Từ (1) và (2) chứng tỏ AB là tiếp tuyến của (I)