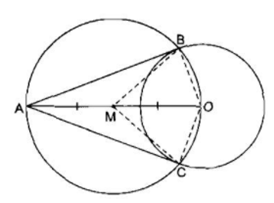
Ta có: MA = MO = MB ( cùng bằng bán kính đường tròn tâm M, bán kính MO)
\(MA{\rm{ }} = {\rm{ }}MB \Rightarrow \Delta MAB\). cân tại \(M \Rightarrow \widehat {BAO} = \widehat {ABM}\)
\(MO = MB \Rightarrow \Delta MOB\) cân tại \(M \Rightarrow \widehat {BOA}{\rm{ }} = \widehat {MBO}\)
\( \Rightarrow \widehat {BAO} + \widehat {BOA} = \widehat {ABM}{\rm{ }} + \widehat {MBO}{\rm{ }} = \widehat {ABO}{\rm{ }}\left( 1 \right)\)
Mặt khác ta lại có: \(\widehat {BAO} + \widehat {BOA} + \widehat {ABO} = {180^o}\,\,\,\,\left( 2 \right)\) (tổng 3 góc trong tam giác)
Từ (1) và (2) \( \Rightarrow \widehat {ABO} = {90^o}\)
Hay AB là tiếp tuyến của (O)
Chứng minh tương tự, ta được AC là tiếp tuyến của (O)