Bài 1. Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (theo câu 1a, đề số 3, §2,3) \( \Rightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha .\)
\(A = \sin \alpha - \sin \alpha .{\cos ^2}\alpha \)
\(\;\;\;\;= \sin \alpha \left( {1 - {{\cos }^2}\alpha } \right)\)
\(\;\;\;\; = \sin \alpha .{\sin ^2}\alpha = {\sin ^3}\alpha \)
Bài 2.
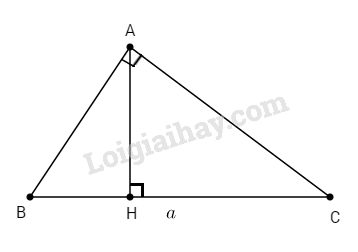
\(∆ABC\) vuông tại A, ta có:
\(AB = AB.{\mathop{\rm cosB}\nolimits} = a.cosB\)
∆AHB vuông tại H, ta có:
\(AH = AB.\sin B = a.\sin B.\cos B\)
Lại có : \(BH = AB.\cos B = a.{\cos ^2}B.\)
Xét tam giác vuông AHC, ta có:
\(CH = AH.\tan \widehat {HAC}\) (mà \(\widehat {HAC} = \widehat B\) vì cùng phụ với \(\widehat C\) )
\( CH= AH.\tan B\)\(\; = a.\sin B.\cos B.{{\sin B} \over {\cos B}} = a.{\sin ^2}B.\)
Bài 3.
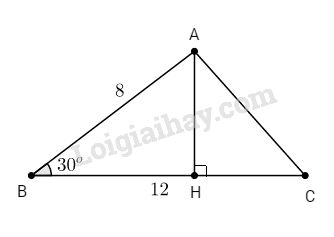
Kẻ đường cao AH của ∆ABC, ta có:
\(AH = AB.\sin B = 8.\sin30^o = 4 (cm)\)
Vậy \({S_{ABC}} = {1 \over 2}.BC.AH = {1 \over 2}.12.4 \)\(\;= 24\,\left( {c{m^2}} \right)\)