Bài 1. Đặt \(A = {{\cos \alpha + \sin \alpha } \over {\cos \alpha - \sin \alpha }}.\) Chia cả tử và mẫu của A cho \(\cos α\), ta có:
\(A = {{1 + \tan \alpha } \over {1 - \tan \alpha }}\)
Thay \(\tan α = 3\), ta có: \({{1 + 3} \over {1 - 3}} = {4 \over { - 2}} = - 2\)
Bài 2.
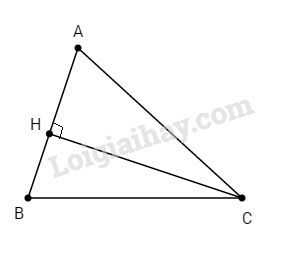
Vẽ \(CH ⊥ AB\), ta có:
\(\eqalign{ & \sin A = {{CH} \over {CA}} \Rightarrow CH = AC.\sin A \cr & {S_{ABC}} = {1 \over 2}AB.CH \cr&\;\;\;\;\;\;\;\;\;= {1 \over 2}AB.AC.\sin A. \cr} \)