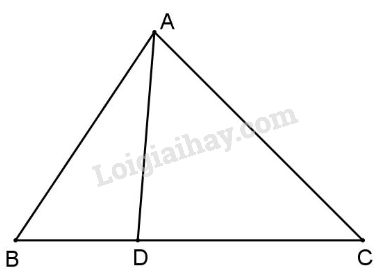
Xét \(\Delta A{\rm{D}}B\), theo bất đẳng thức tam giác
\(A{\rm{D}} > AB - B{\rm{D}}\) (1)
Tương tự đối với \(\Delta A{\rm{D}}C\)
\(A{\rm{D}} > AC - DC\) (2)
Công từng vế của (1) và (2) ta có:
\(2A{\rm{D}} > AB + AC - (B{\rm{D}} + C{\rm{D}})\)
hay \(2A{\rm{D}} > AB + AC - BC\)
\( \Rightarrow A{\rm{D}} > \dfrac{{AB + AC - BC}}{2}\).
Chứng minh tương tự ta có\(A{\rm{D < AB + BD}}\) và \(A{\rm{D}} < AC + DC\)
\(\eqalign{ & \Rightarrow 2AD < AB + AC + (BD + DC)\cr& \Rightarrow 2AD < AB + AC + BC \cr & \Rightarrow AD < {{AB + AC + BC} \over 2}. \cr} \)
Vậy \(\dfrac{{AB + AC - BC} }{ 2} < AD < \dfrac{{AB + AC + BC} }{ 2}.\)