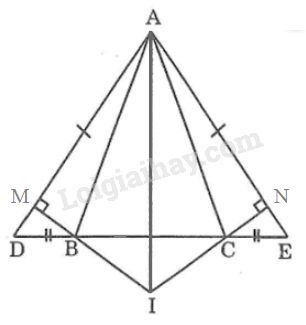
Xét \(∆ABD\) và \(∆ACE\) có:
\(AD = AE\) (vì \(∆ADE\) cân tại \(A\))
\(\widehat D = \widehat E\) (vì \(∆ADE\) cân tại \(A\))
\(DB = EC\) (gt)
\( \Rightarrow ∆ABD = ∆ACE\) (c.g.c)
\( \Rightarrow AB = AC\) (hai cạnh tương ứng).
Vậy \(∆ABC\) cân tại \(A.\)
b) Xét hai tam giác vuông \(BMD\) và \(CNE\) có:
\(\widehat {BM{\rm{D}}} = \widehat {CNE} = 90^\circ \)
\(BD = CE\) (gt)
\(\widehat D = \widehat E\) (vì \(∆ADE\) cân tại \(A\))
\( \Rightarrow ∆BMD = ∆CNE\) (cạnh huyền - góc nhọn)
\( \Rightarrow BM = CN\) (hai cạnh tương ứng).
c) \( ∆BMD = ∆CNE\) (chứng minh trên)
\( \Rightarrow \widehat {DBM} = \widehat {ECN}\) (hai góc tương ứng) (1)
\(\widehat {DBM} = \widehat {IBC}\) (đối đỉnh) (2)
\(\widehat {ECN} = \widehat {ICB}\) (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra \(\widehat {IBC} = \widehat {ICB}\) hay \(∆IBC\) cân tại \(I.\)
d) Xét \(∆ABI\) và \(∆ACI\) có:
\(AB = AC\) (chứng minh trên)
\(IB = IC\) (vì \(∆IBC\) cân tại \(I\))
\(AI\) cạnh chung
\( \Rightarrow ∆ABI = ∆ACI\) (c.c.c)
\( \Rightarrow \widehat {BAI} = \widehat {CAI}\) (hai góc tương ứng).
Vậy \(AI\) là tia phân giác của \(\widehat {BAC}\).